고정 헤더 영역
상세 컨텐츠
본문 제목
[Practical Statistics for Data Scientists] A팀: Naive Bayes Classification & Discriminant Analysis
본문
# Naive Bayes Classification
나이브 베이즈 분류 는 말 그대로 베이즈 분류 ( Complete ( or Exact ) Bayesian Classification ) 의 Naive 한 버전인데, 이는 나이브 베이즈 분류에서 Y = i ( i = 0 또는 1 ) 이 주어졌을 때 예측변수 X들이 모두 독립이라는 'Naive' 한 가정을 통해 계산을 단순화하기 때문이라고 생각하면 이해가 쉽습니다.
나이브 베이즈 분류의 목적은 당연히 X가 주어졌을 때 Y값의 예측 ( Y=i 일 확률의 예측 ) 이고, 이를 아래처럼 표현할 수 있습니다.
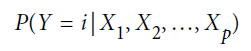
여기서 나이브 베이즈의 핵심은 Y가 주어졌을 때 X=x일 확률 을 사용해 위 목표를 달성한다는 것입니다. 나이브 베이즈의 계산 절차를 설명하기 전에, 베이즈 정리에 대해 잠시 알아볼 필요가 있습니다.
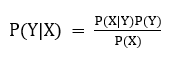
어렵게 생각할 필요 없이, 우리는 좌변에서의 X,Y 순서와 우변에서의 X, Y 순서가 바뀐 것만 이해하면 됩니다. 조건부 확률 부분의 연산이 헷갈린다면 다음 식을 보면 됩니다.

이제, 나이브 베이즈 분류는 아래 식과 같이 진행됩니다.
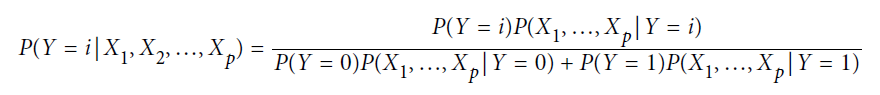
[식 2]는 위에 나왔던 [식 1] 과 동일한 형태인데, Y = i ( 0 또는 1 ) 의 값을 갖고 예측 변수 X가 P가지라는 가정 하에 직관적으로 비교가 가능합니다.
[식 2]의 분모 부분을 이해하려면 전확률의 공식을 알면 좋습니다.


요약하면, A를 A와 B의 겹치는 부분의 합으로 표현하겠다는 말입니다. 물론 k개의 B는 표본공간 S를 빠지는 부분 없이 분할한다는 가정이 필요합니다.
이를 [식 2]에 적용하면, 아래와 같이 표현할 수 있으므로 이제 [식2] 를 이해할 수 있습니다.

위에서 설명했듯 나이브 베이즈는 Y값이 주어졌을 때 P개의 예측변수 X가 서로 독립이라는 'Naive'한 가정을 가지므로 [식2] 를 여러 확률의 곱으로 쪼갤 수 있습니다.

[식 4]까지 구했다면 이제는 실제 계산만이 남았는데 각 확률은 주어진 train set 에서 해당 조건을 만족하는 observation들의 비율로 구하면 됩니다. 실제 적용 부분은 생략합니다.
# Discriminant Analysis
Discriminant Analysis는 여러 모집단으로부터 추출한 표본에서 표본이 가진 정보를 이용해 분류 기준(Allocation Rule)을 만듭니다. 책에서 설명하는 부분은 그중에서도 Fisher's Linear Discriminant Analysis 에 관한 내용입니다.
두 개의 그룹에서 표본을 추출했다는 가정 하에, Fisher's LDA는 좋은 분류 기준을 만들기 위해
데이터의 편차를 2가지 -> [그룹 간 편차] 와 [그룹 내 편차] 로 나눕니다. 분류가 잘 되었다는 것은 [그룹 간 편차] / [그룹 내 편차] 가 크다는 말로 해석할 수 있으므로 이 값을 최대화하는 분류 기준을 세워야 합니다.
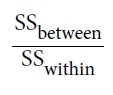
P개의 예측변수(X)를 종합적으로 고려해야 하므로 이들을 선형결합 하여 아래와 같이 사용합니다.

두 개의 그룹에 대한 분류 기준을 세우고 있으므로, [식5] 를 아래와 같이 표현할 수 있습니다.
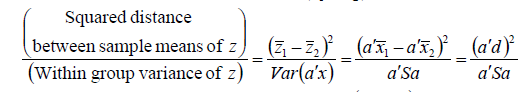
** S는 X의 표본 공분산행렬이고, d는 두 그룹에서 나온 표본의 평균의 차이입니다.
이후, 'Maximization Lemma' 에 의해 [식 7] 을 최대화하는 a(분류 기준, p차원 벡터 x를 스칼라로 만들 가중치 벡터) 는 다음과 같이 계산됩니다.

** 계산 및 구현은 수혁님께서 꼼꼼히 잘 설명해주셔서, 염치없지만 조금 다른 내용 위주로 글을 채웠습니다. :)





댓글 영역