[Practical Statistics for Data Scientists] A팀: Strategies for Imbalanced Data

Undersampling (Downsampling)

Undersampling : 분류 모델에서 가지고 있는 것의 class 정보를 보다 적게 사용하는 것.

 

데이터가 충분히 많은 경우, undersampling을 이용해 데이터를 0과 1 사이로 더 균형있게 모델링 할 수 있다. Undersampling을 사용하는 이유는 dominant class의 데이터가 많은 중복 값을 가지기 때문이다. 즉, 대부분의 데이터는 0과 1의 class 비율이 50:50이 아닌 불균형한 데이터를 가진 경우가 많기 때문에 이를 50:50으로 만들어주는 것이다.

Undersampling을 이용해 중복되는 값을 제거해 더 작고 균형있는 데이터를 사용할 경우 모델의 성능을 향상할 수 있을 뿐 아니라 데이터를 더 쉽게 다룰 수 있으며 모델을 탐색하는데도 도움이 된다. 

그렇다면 어느 정도까지 undersampling을 해야할까? 일반적으로 dominant class에 대해 수 만개의 데이터 정도면 충분하다고 알려져 있다. 또한 class를 구분할 때, 0과 1이 더 쉽게 구분될수록 더 적은 데이터로도 충분히 좋은 결과를 낼 수 있다. 

 

아래는 실제 불균형 데이터를 R을 이용해 분류예측에 사용한 결과이다. 

mean(full_train_set$outcome=='default')
[1] 0.1889455

full_model <- glm(outcome ~ payment_inc_ratio + purpose_ + home_  
                  + emp_len_+ dti + revol_bal + revol_util, data=full_train_set, 
                  family='binomial')
pred <- predict(full_model)
mean(pred > 0)
[1] 0.003942094

위 실험에서 사용한 데이터는 채무이행자와 불이행자인데 default가 채무불이행을 뜻한다. 현재 전체 데이터의 약 19%가 채무불이행임을 확인할 수 있다. 하지만 이 데이터셋을 이용해 모델을 학습하면 약 0.39%의 경우만이 채무불이행이라고 예측되는 것을 확인할 수 있다. 

반면 실제로 downsampling을 이용해 데이터 균형을 맞춘 후 다시 모델을 학습하면 예상했던 것처럼 약 50%가 채무불이행이라고 판단된다. 

이처럼 데이터의 불균형을 해소하는 것은 모델의 학습의 중요한 요소 중 하나가 될 수 있다. 

 

 

Oversampling and Up/Down Weighting

Oversampling (Upsampling) : rare한 class의 데이터를 더 늘리는 기법. 필요할 경우 부트스트랩을 사용하기도 한다.

Up weight or down weight : rare한 class에 더 큰 가중치를 부여하거나 prevalent한 class에 더 적은 가중치를 부여하는 것.

 

Undersampling에 대한 한 가지 비판적 시각은 데이터를 버리기 때문에 수중에 있는 모든 정보를 사용하지 않는다는 것이다. 특히 전체 데이터 크기가 더 작을수록 애초에 데이터에서 얻을 수 있는 정보가 더 한정적인데, 이때 더 많은 데이터를 가진 class를 undersampling 하는 것은 중요한 정보를 그대로 버리게 되는 것일 가능성이 커진다. 이 경우 더 많은 데이터를 가진 class에 대해 undersampling하는 대신 부트스트랩 등을 사용해 더 데이터가 적은 class를 upsampling하는 것이 더 효과적이다. 

 

또한 데이터에 가중치를 부여하는 것도 up/down sampling과 비슷한 효과를 얻을 수 있다. 

아래는 가중치를 부여해 R로 실험을 진행한 결과이다.

wt <- ifelse(full_train_set$outcome=='default', 1 / mean(full_train_set$outcome == 'default'), 1)
full_model <- glm(outcome ~ payment_inc_ratio + purpose_ + home_ +
		emp_len_+ dti + revol_bal + revol_util,
 		data=full_train_set, weight=wt, family='quasibinomial')
pred <- predict(full_model)
mean(pred > 0)
[1] 0.5767208

여기서 채무불이행에 대한 가중치는 1/p (>1)로 설정되며 이때 p는 채무불이행 확률이다. 또한 채무이행에 대한 가중치는 1이다. 데이터 전체로 보면 채무불이행과 채무이행의 가중치 합은 거의 같다. 이렇게 가중치를 부여하고 다시 모델을 실행해보면 위에서 0.39%가 나왔던 것과 달리 약 58%의 확률이 나오는 것을 볼 수 있다.

 

Data Generation

우리가 사용하는 데이터들을 그 집단의 전체가 아닌 일부를 나타낸다고 볼 수 있다. 즉, 관찰된 데이터에만 기반해 학습을 수행한다는 것이다. 이러한 학습의 한계를 극복하기 위해 나온것이 바로 데이터 생성이다. 

데이터 생성은 부트스트랩 등의 기법을 이용해 기존의 데이터와 비슷하지만 같지는 않은 새로운 데이터를 만들어 내는 것을 말한다. 이는 upsampling을 할 때 사용되기도 한다. 이렇게 생성된 새로운 데이터를 학습에 추가적으로 이용할 경우 보다 강력한 규칙들을 학습할 수 있게 된다. 

이 기법은 SMOTE 알고리즘이 등장하면서 설득력을 얻게 되었는데 SMOTE 알고리즘이란 부트스트랩이나 KNN 모델 기법을 활용한 알고리즘으로 전체 과정은 다음과 같다. 다음은 KNN을 이용한 방법이다. 

 

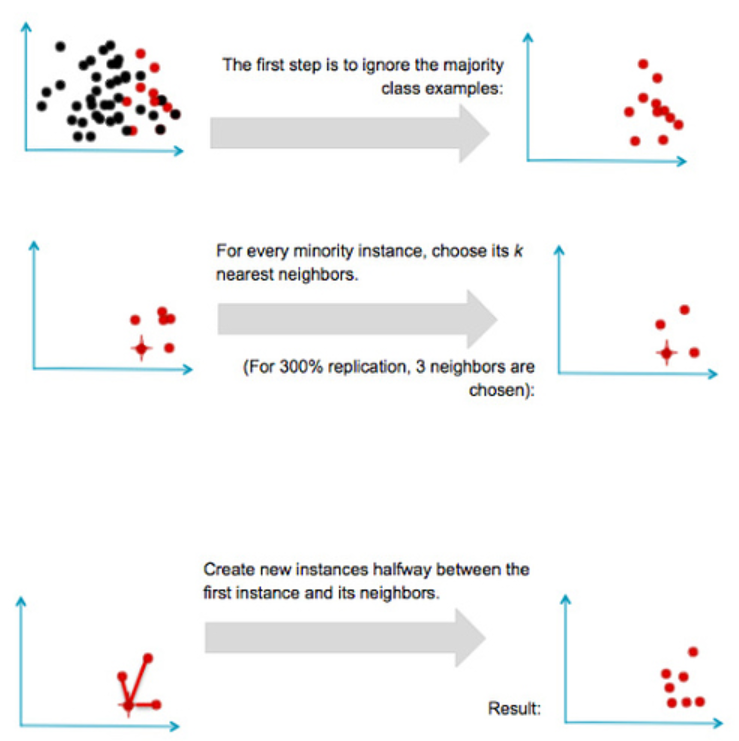
이러한 SMOTE 알고리듬은 FNN 패키지를 사용하여 R에서 직접 구현할 수도 있다.

 

Cost-Based Classifcation

실제로 분류를 실행할 경우, 정확성과 AUC는 분류 규칙을 선택하는 가장 간단한 방법 중 하나이다. 종종 estimated cost는 false positives 대 false negatives로 할당될 수 있으며, 1과 0을 분류할 때 최선의 컷오프를 결정하기 위해 이러한 비용을 통합해 사용하는 것이 더 좋다. 예를 들어, 새로운 대출의 채무불이행의 예상원가는 C이고 상환된 대출의 기대수익은 R이라고 가정하자. 그러면 그 대여금에 대한 기대수익은 다음과 같다.

기대수익률 = P(Y = 0) × R + P(Y = 1) × C

이 경우 단순히 대출금을 채무불이행 또는 상환으로 표기하거나 채무불이행 발생 확률을 판단하는 대신 대출에 긍정적 기대수익률이 있는지를 판단하는 것이 더 타당하다. 예측된 채무불이행 확률은 중간 단계로, 대출의 총액과 결합해야 사업의 궁극적인 계획 지표인 기대이익을 결정할 수 있다. 예를 들어, 예측된 채무불이행 확률이 약간 높은 더 큰 대출에 유리하도록 작은 가치의 대출은 넘어갈 수 있다.

 

Exploring the Predictions

AUC와 같은 하나의 측정 기준만으로는 상황에 대한 모델의 적합성의 모든 측면을 평가할 수 없다. 그림 5-8은 대출 데이터에 적합한 네 가지 다른 모델에 대한 결정 규칙을 두 가지 예측 변수(borrower_score & pay ment_inc_ratio)를 사용해 보여준다. 모델은 linear discriminant analysis (LDA), logistic linear regression, logistic regression fit using a generalized additive model (GAM), tree model 이렇게 4가지가 사용되었다. 선의 왼쪽 위에 있는 영역은 예측된 기본값에 해당하며 이 경우 LDA 및 로지스틱 선형 회귀 분석에서 거의 동일한 결과를 얻은 것을 볼 수 있다. 트리 모형은 두 단계로 이루어진 least regular rule을 생성하며 마지막으로, 로지스틱 회귀 분석의 GAM 적합도는 트리 모델과 선형 모델 간의 절충을 나타낸다.