[분류 예측 스터디] 핸즈온 9장 비지도 학습

1. Unsupervised vs Supervied

인공지능 AI

• supervised learning (지도학습) :  정답(label)이 있는 데이터를 활용한 학습 | ex) 분류 & 회귀
• unsupervised learning (비지도학습) : 정답이 없는 데이터로 학습, feature들의 비슷한 정도를 이용하여 군집

주로 데이터의 패턴과 형태를 분석하는 것이 중요하다.

unsupervied learning은 대표적인 것이 "군집"인데, 다양한 알고리즘을 통해 군집화를 할 수 있다.

ex) K means , density estimation, expectation maximization, parzen window, DBSCAN, 차원 축소

 

• density estimation : 밀도 추정 - 데이터로부터 데이터의 분포, 밀도(확률)을 추정
  • 지도학습은 모든 데이터의 PDF가 gaussain이라는 가정하에 가중치를 계산하게 된다.
  • but, 실제로는 그렇지 않기에, 밀도함수를 추정해야하는 데, 이 역시 비지도 학습의 예시이다.
  • ex) KDE- parzen window
• EM(expectation maximization) - GMM과 관련된 알고리즘
  • 모르는 모수(확률분포의 매개변수)에 대한 최대우도 추정치(MLE)를 찾고자 하는 알고리즘

[Clustering]

1. introduction : clustering vs classification

• Classification  = 지도학습 - 이미 분류가 되어 있는 라벨의 데이터들을 학습하여, 새로운 데이터의 라벨을 예측한다.
• Clustering = 비지도 학습 - 데이터의 feature의 패턴과 유사도를 계산하여, group을 만든다.

그림의 왼쪽과 같이, 라벨이 없는 데이터의 feature들을 파악하여, 왼쪽과 같은 형태의 cluster를 형성하는 것이 목적이다.

2. Algorithm2 : K means

1. 군집의 개수 K 설정
2. 초기 중심점(centroid) 설정
3. 데이터를 군집에 할당 및 배정
4. centroid 갱신
5. 데이터를 군집에 재할당, 배정

4~5번 과정을 더 이상 centroid가 갱신이 되지 않을 때까지 반복한다.

 

생각해야할 issue들

• 군집 개수 K 설정 : hyperparameter tuning
• 초기 중심점 설정 방법 : randomly, manually, k-means++
• 데이터를 군집에 할당 : "거리" 상 가장 가까운 군집에 할당한다.
• 할당된 군집에서 재설정 : centroid를 군집 속, 가장 중간(평균)으로 재설정한다.

from sklearn.datasets import make_blobs

 

blob dataset

 

2-1. 학습 및 예측 and 결정 경계

from sklearn.cluster import KMeans

k = 5 ## 사전에 정해야한다.
kmeans = KMeans(n_clusters=k, random_state=42)
y_pred = kmeans.fit_predict(X)

 

[K means를 사용하여 분류한 결과물]

2-2. hard vs soft

hard clustering : 하나의 데이터가 정확히 하나의 군집에 할당soft clustering : 하나의 데이터가 다수의 군집에 할당하는 것

K -means의 경우, hard clustering에 해당한다.

모든 데이터가 다수의 clsuter에 중복으로 해당하는 것이 아닌, 단 하나의 cluser에 할당하도록 만든다.

Hard clustering은 특히 "가장 가까운 centroid"선택 : 거리 계산을 해야한다.

kmeans.transform(X_new)
array([[2.81093633, 0.32995317, 2.9042344 , 1.49439034, 2.88633901],
       [5.80730058, 2.80290755, 5.84739223, 4.4759332 , 5.84236351],
       [1.21475352, 3.29399768, 0.29040966, 1.69136631, 1.71086031],
       [0.72581411, 3.21806371, 0.36159148, 1.54808703, 1.21567622]])

4개의 sample(X_new)에 대해, 5개의 군집, 즉 5개의 centroid에 대한 거리 결과물을 저장한다.

이는 "유클리안 거리"를 이용한 것이다.

 

 

 

2-3. 성능 평가 지수 : inertia(이너셔)

inertia_ "군집화 이후에, 각 centroid에서 군집 내, 데이터 간의 거리를 합산, 즉 군집의 응집도를 표현"

"작을 수록 응집도가 높게 된 것 이므로, 군집화가 잘 됐다고 할 수 있다."

kmeans.inertia_
211.5985372581684

kmenas.transform :각 데이터의 5개 centroid 별로 거리 값들을 모두 계산한 것들을 반환해준다

X_dist = kmeans.transform(X) ##계산된 centorid와의 거리값들
X_dist ##cluster index 별로 거리들

array([[0.46779778, 3.04611916, 1.45402521, 1.54944305, 0.11146795],
       [0.07122059, 3.11541584, 0.99002955, 1.48612753, 0.51431557],
       [3.81713488, 1.32016676, 4.09069201, 2.67154781, 3.76340605],
       ...,
       [0.92830156, 3.04886464, 0.06769209, 1.40795651, 1.42865797],
       [3.10300136, 0.14895409, 3.05913478, 1.71125   , 3.23385668],
       [0.22700281, 2.8625311 , 0.85434589, 1.21678483, 0.67518173]])

score() 매서드는 "큰 값이 좋은 것"이라는 가정이 있기에, 이를 만족하기 위해, 각 sample들의 centroid에 대한 거리들을 모두 음수로 만든다. 즉 거리가 제일 작은 것이 제일 큰 것이 되고, 이를 합산하니 음수로 출력이 된다.

kmeans.score(X)
-211.59853725816836

 

 

2-4. 알고리즘 및 매개변수 설명

kmeans_iter1 = KMeans(n_clusters=5, init="random", n_init=1,
                      algorithm="full", max_iter=1, random_state=0)
kmeans_iter2 = KMeans(n_clusters=5, init="random", n_init=1,
                      algorithm="full", max_iter=2, random_state=0)
kmeans_iter3 = KMeans(n_clusters=5, init="random", n_init=1,
                      algorithm="full", max_iter=3, random_state=0)
kmeans_iter1.fit(X)
kmeans_iter2.fit(X)
kmeans_iter3.fit(X)

[k-means 반복 횟수에 따른 변화]

그림 설명 : 가장 맨 윗줄의 오른쪽이 반복 횟수 1번이다. 두번째 행은 왼쪽이 반복횟수 1번, 오른쪽이 반복횟수 2번이다. 세번째 행은 왼쪽이 반복횟수 2번, 오른쪽이 반복횟수 3번이다.

 

반복 횟수 1~3으로 갈수록, centroid의 위치도 조정이 되고, 결정경계도 점점 정확해 져가는 것을 관찰할 수 있다.

 

 

 

2-5. As problem : K mean의 변동성

kmeans_rnd_init1 = KMeans(n_clusters=5, init="random", n_init=1,algorithm="full", random_state=2)

kmeans 클래스의 default 매개변수를 살펴보면 다음과 같다.

• n_clusters : 군집화를 할 K 값
• init : 초기 centroid를 설정하는 방법
• n_init : centroid 선택 및 시도 횟수
• algorithm : k-means 알고리즘 선택

init : "random"

kmeans_rnd_init1 = KMeans(n_clusters=5, init="random", n_init=1,
                          algorithm="full", random_state=2)
kmeans_rnd_init2 = KMeans(n_clusters=5, init="random", n_init=1,
                          algorithm="full", random_state=5)

초기 centroid를 잡는 방법은 random으로 하기 때문에, random seed가 바뀌면 다른 결과가 나온다.

따라서 random seed를 고정했다고 해서, 그것이 정답이 아닐 수도 있다!!

 

[random_state 변화에 따른 결과가 달라지는 모습]

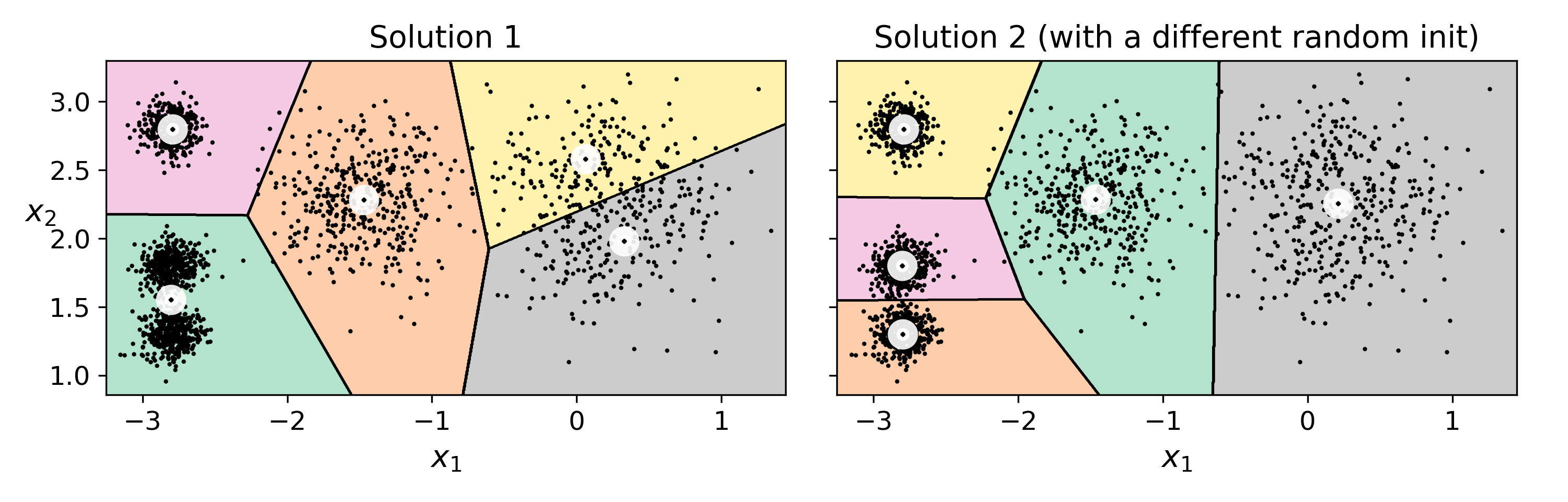
그렇다면 어떻게 해결해야할까?

해결 방법은 다음과 같이 대표적으로 2가지가 있다. 

2-6. 변동성 해결 방법 1: 다중 초기화 

n_init : 1 이상

n_init이 1 이상이라는 것은 초기 centroid를 무작위로 5개를 뽑는 시도를 여러번 하는 것이다.

여러번 시도 후, 제일 좋은 것의 결과물을 선택한다.

이때는 random_state가 같기에, 최종 결과물이 같게 나오지만, 

n_init = 1과 비교했을 때, 더 나은 성능을 보인다.

kmeans_rnd_10_inits = KMeans(n_clusters=5, init="random", n_init=10,
                             algorithm="full", random_state=2)
kmeans_rnd_10_inits.fit(X)

[random_state가 같고, n_init = 10으로 증가시켰을 때 모습]

kmeans_rnd_init1.inertia_
219.43539442771396

kmeans_rnd_10_inits.inertia_
211.5985372581684

실제로 성능이 더 나아진 것을 볼 수 있다.

 

2-7. 변동성 해결방법  2: stohastic 초기화  - k means ++

이번에는 centroid를 단순 무작위로 추출하는 것이 아니라, sample과의 거리를 고려하여

확률적, stochastic한 방법으로 centroid를 추출하는 방법을 사용해보자.

1. 데이터 집합으로부터 임의의 데이터를 하나 선택하여 첫 번째 중심으로 설정한다.
2. k개의 중심이 선택될 때까지 다음의 단계를 반복한다
   1. 데이터 집합의 각 데이터에 대해서, 해당 데이터와 선택된 중심점들 중 가장 가까운 중심과의 거리 D(x)를 계산한다.
   2. 확률이 D(x)^2에 비례하는 편중 확률 분포를 사용하여 임의의 데이터를 선택한 후, n번째 중심으로 설정한다.
3. 선택된 k개의 중심들을 초기 값으로 하여 k-평균 클러스터링을 수행한다.

결과적으로, 이전에 선택한 centroid와 거리가 큰 점이 높은 확률로 선택되도록 한다.단순, 랜덤으로 추출한 k개의 centroid는 전체 분포를 고려하지 못하고 몰릴 수 있는 문제를 가지고 있다.

kmeans_rnd_10_inits = KMeans(n_clusters=5, init="k-means++", n_init=10,
                             algorithm="full", random_state=2)

2-8. 최적의 k 값 찾기

k 값에 따라 군집되는 정도가 달라지는데, 이는 데이터 분포를 보고 사용자가 정할 수 밖에 없다.

즉, hyperparameter로 tunning의 대상이 된다.

 

k값에 따른 군집화 비교

[k = 3과 k=8의 군집화 비교]

앞서 k=5에 비해, k=3은 너무 군집화가 되지 않았고, 8일때는 너무 자세하게 나누어, 굳이 나누지 않아도 될 군집도 나누어졌다.

print("k3_inertia : ",kmeans_k3.inertia_, "|","k8_inertia", kmeans_k8.inertia_)
k3_inertia :  653.216719002155 | k8_inertia 119.11983416102879

단순하게 inertia값만 보면 k 값이 커질 수록, 전체 데이터 분포에 centorid 개수가 증가하는 것이기 때문에,

centroid에 대한 데이터들의 가장 가까운 거리의 합이 감소하기 마련이다.

 

단순하게 작아지는 inertia만 보고 k값을 정할 수 없다. 

작아지는 변화 양항을 관찰해야한다.

 

Elbow Graph

[k 값에 따른 inertia값의 변화 양상]

k = 4일 때가 elbow인데, 이보다 더 커지면 inertia값이 작아지는 기울기가 그리 크지 않다.

이는 k값에 증가에 따른 성능 향상 효과가 효율적이지 않다는 것이다.

눈으로 관찰했을 때는 k = 4가 적당하나, 실제로 데이터 분포를 보면 k = 5가 더 좋은 것 같다.

다른 방법으로 k값을 정해보자

 

Silhouette coefficient

각 데이터 포인트와 주위 데이터 간의 거리 계산을 통해 얻은 값

centroid와의 거리를 이용한 inertia와 다르게 주위 데이터 분포, 거리를 이용하기에 응집도를 더 구체적으로 표현이 가능하다.

군집 내 비유사성("wthin" dissimilarites)은 작고, 군집 간 비유사성("between" dissimilarities)은 커야 생성된 클러스터의 품질이 좋다고 할 수 있다.

Peter J.Rousseeuw (1987), Silhouettes: a graphical aid to the interpretation and validation of cluster analysis , Computational and Applied Mathematics 20: 53-65

 

계산 : (b-a)/ max(a,b)

• a: 같은 클러스터에 있는 다른 샘플까지의 평균 거리(군집 내부 평균 거리) - 최소화 대상
• b : 가장 가까운 군집까지의 평균 거리(자신의 군집을 제외한) - 최대화 대상

장점 : 군집화 이후에 계수를 구하기에, 군집화 알고리즘에 영향을 받지 않는다.

단점 :

• 데이터양이 많을 수록 계산 시간이 오래걸린다.
•  전체 데이터의 실루엣 평균값만 가지고 판단은 불가능, 클러스터링 별로의 평균값도 관찰해야한다.

[k값에 따른 실루엣 값 변화]

k = 4일때 최대이므로 좋은 것이지만, k = 5도 나쁘지 않은 선택이라는 것을 알 수 있다.

실루엣 계산 자체가 거리들의 평균을 이용하기에 원형 클러스터를 대표할 수 있지만

원형이 아닌 클러스터일 경우, 클러스터에서 가장 멀리 떨어진 데이터에 영향을 받기 쉽다.

but, 이 역시도 cluster 모양이 "원형"이라는 가정에 기반한다.

원형이 아니라면 맞지 않는다.

각 cluster의 샘플별로 실루엣을 계산하여, index 별로 실루엣 계수를 구해보자

• 그래프의 너비(세로) : 클러스터 내 데이터 개수
• 그래프의 높이(가로) : 실루엣 계수
• 빨간색 선 : 전체 실루엣 평균 점수

해당 선보다 특정 클러스터의 점수가 작다면, 클러스터 샘플이 다른 클러스터랑 너무 가깝다는 것을 의미한다.(즉, 구별될 수 있는데, 구별하지 않았거나, 구별할 필요가 없는데, 구별하였을 때)

결과적으로 나누어진, 군집간의 거리가 너무 가까워진다.

내부 응집도도 감소하고, 다른 군집과의 거리도 가까워지고

 

 

2-11. k - means의 한계

cluster가 원의 모양을 띈 상황은 잘 적용이 되나, 

 

random initial 일때, 원형이 아닌 데이터 분포에 대해 취약하다.

원형의 클러스터를 찾으려고 하는 k mean의 특성 때문에..

feature간의 스케일을 맞추면, 좀 더 구형태의 분포가 될 것이다

 

2-12. 실제 적용

군집을 사용한 이미지 분활

군집을 사용한 전처리

군집은 차원 축소에 효과적인 방법,

지도 학습 전에, 전처리 단계로 사용할 수 있다.

즉, 차원 축소의 효과처럼, 군집으로 feature의 개수를 줄인다라는 아이디어.

feature의 패턴을 관찰하여, 가장 대표적인 feature로서, 군집을 형성

아님, 더 나아가 군집된 labeling을 실제 label로 분류 지도 학습 데이터 전처리로 바꿀 수도 있다.

 

군집을 사용한 준비지도 학습

잠깐 언급했던 군집 사용의 응용 : 라벨링의 대체

레이블이 없는 데이터가 많고, 레이블이 있는 데이터가 적을 때, 준지도 학습을 사용한다.

기본적으로 준지도학습의 loss는 지도와 비지도 학습의 loss를 합이 된다.

단순 50개의 데이터 셋은 선별한 것과 다른 점은

이 50개의 이미지는 각 군집을 **대표**하는 것이기에, 전체를 더 좋게 표현할 수 있다.

좋은 sample의 50개이다.

로지스틱 회귀를 사용하면 결과가 더 좋아질 수 있음을 알 수 있다.

 

reference:

https://github.com/rickiepark/handson-ml2/blob/master/09_unsupervised_learning.ipynb