[강화학습 스터디] Introduction to Reinforcement Learning

Naive Concept

1. Introduction
2. OpenAI Gym

Mathematical concept

1. 벨만 방정식
2. 마르코프 체인

---

1. Introduction

1) 강화학습(reinforcement learning)이란?

 : computational approach to learning from interaction

• STATE(상태)
• ACTION(행동)
• REWARD(보상)

이렇게 3가지의 가장 기본적인 개념으로 구성되는 시스템이라고 볼 수 있다. 환경과의 상호작용(보상)을 통해 새로운 행동을 취하고, 그에 따라 계속적으로 변하는 상태라고 이해할 수 있다. 

출처 : https://youtu.be/JMpslE8GtCo

출처 : hunkim.github.io/ml/

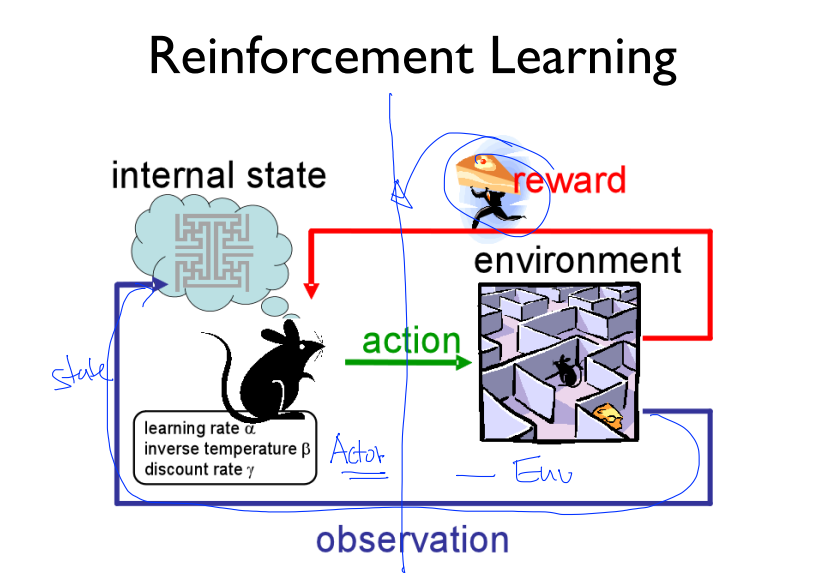
2) 강화학습의 적용/응용 연구 분야

• Robotics : 관절에 걸리는 돌림힘(토크) 계산
• Business operations
  • 재고 관리
  • 자원 할당 (ex)콜센터 서비스 대상 선정
• Finance
  • 투자 결정
  • 포트폴리오 디자인
• E- commerce / media
  • 조회수/시간 = reward → 콘텐츠 선정
  • 피로도 절감 → 광고 선정
• 가장 유명한(?) 강화학습 연구
  • alphaGO

alphago image

2. OpenAI Gym

: 강화학습을 학습할 수 있는 간단한 게임들부터, 복잡한 강화학습 모델에 대한 환경까지 모두 제공하고 있는 파이썬 라이브러리이다. 여기에서는 강의에서 소개한 간단한 입문용 게임 몇개를 예시로 가져왔다. 

• 팩맨

https://www.notion.so/Day-1-184dfa016b7e47f49bda880718beb98a#81fb2992917b42b5b767c8292e0f178a

• Frozen Lake

출처 : hunkim.github.io/ml/

출처 : hunkim.github.io/ml/

출처 : hunkim.github.io/ml/

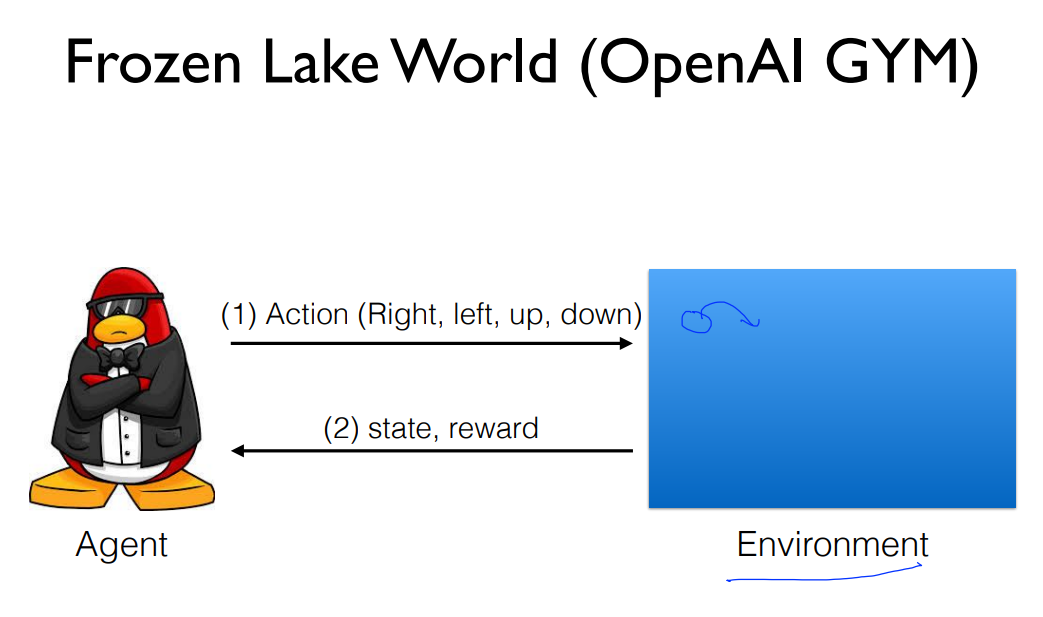
https://www.notion.so/Day-1-184dfa016b7e47f49bda880718beb98a#314ad1b19af748aebabd8586cc031e00

https://www.notion.so/Day-1-184dfa016b7e47f49bda880718beb98a#30c1773c827441afbde265bf208ffed2

 

3. Bellman Equation : 벨만 방정식

1) 동적 계획법 (Dynamic Programming) : 동적 프로그래밍은 어디선가 여러번 들어봤을 말이지만, 이를 설명하기 위해 강화학습만큼 밀접한 관계를 맺고 있는 분야도 없다. 하나의 복잡한 문제(미로를 탈출하기)를 해결하기 위해, 작은 문제로 쪼개서 해결하는 재귀적 방식(단계마다 보상을 확인하는 방식)이라고 동적 계획법을 아주 간단하게 설명할 수 있다. 

2) 벨만 방정식 : Deterministic world에 대해서

: non-deterministic world 인 경우, state에 따른 reward가 항상 정해져있지 않고 가변적이므로 조금 더 복잡한 식을 사용하게 된다. 

벨만 방정식. 위에서도 거듭 설명한 내용을 수식으로 표현하자면 이렇다.

• R(s,a) = state(s)에서 새로 취하는 action(a)에 따른 보상(R)
• V(s') = state(s)에서 취한 action(a)따라 변하는 새로운 상태(s')
• max(a)는 'a에 따른 최대값을 찾아주자'의 의미.
• gamma 값의 설정 : 0.9 ~ 0.99 사이의 값으로, 낮을 수록 단기간의 보상에 따른 결정을 지향하게 되고, 높을 수록 장기간의 보상을 기대한 행동을 취하게 할 수 있다. 

도착지점부터 한 단계씩 되돌아가면서 작성할 수 있다.

 

4. Markov Chain / MDP(Markov Decision Process)

https://www.notion.so/Day-1-184dfa016b7e47f49bda880718beb98a#4efcb1455e134dd699b1e8681a2a5e8c

• MDP : 마르코프 의사 결정 과정
  • 마르코프 체인 / 프로세스: 과거 상태(s(t-2),s(t-1))들과 현재 상태(s(t))가 연속적으로 주어졌을 때, 미래 상태(s(t+1))가 과거 상태와는 독립적으로 현재 상태에 의해서만 결정되는 특성을 마르코프 특성이라고 한다.
  • : 마르코프 특성을 지니는 이산시간 확률 과정
  • 즉, MDP = 마르코프 체인 + 결정 + 보상 (aka. 마르코프 체인의 확장판)
• Markov Property : 마르코프 특성이란?
  
  • 이산적인 상태(비연속적)가 있다고 할 때, 전체 상태 s = {s1, s2, s3, ...} 라고 하자.
  • 조건부 확률 P(s(t+1)|s(t)) = t번째 상태에서 t+1번째 상태로 갈때의 특정 상태(s)가 될 확률

• 상태 변이 확률 Pss' = 상태(s)에서 어떤 상태(s')로 변할 확률로 (s=s'인 경우와 아닌 경우를 모두 포함하는 식)

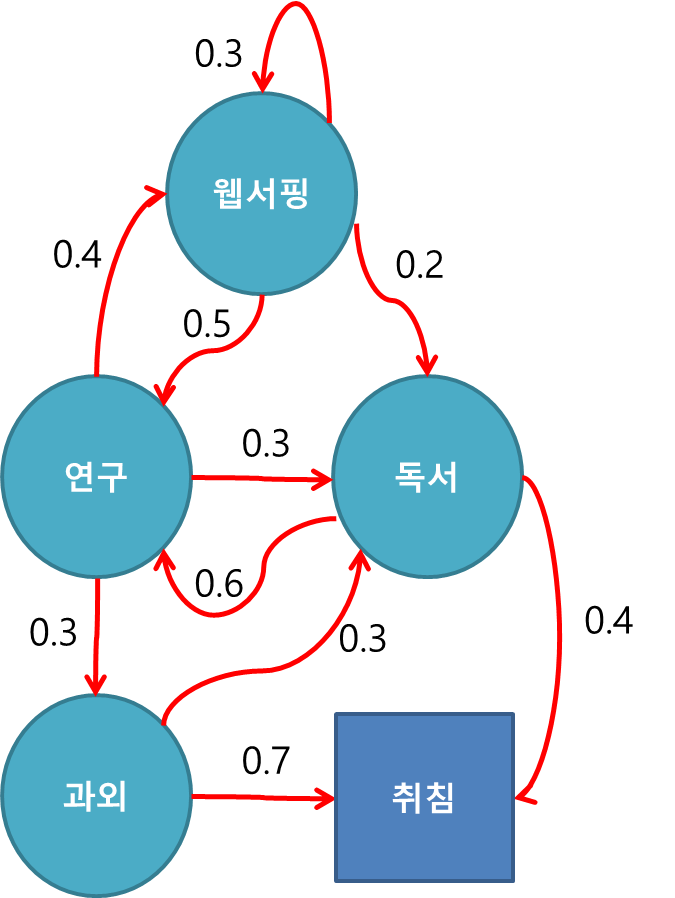
• 예시 1)  총 5개의 상태(웹서핑, 연구, 독서, 과외, 취침)에 대해서, 한 상태에서 다른 상태로 변할 확률(상태 변이확률)은 빨간색 화살표 위에 각각 적혀 있는 값으로, 해당 확률로 상태 변화가 일어날 때, 이러한 상황을 마르코프 과정이라고 한다. 우측은 그러한 상태 변이 확률들을 하나의 행렬로 표현한 것으로, 상태 변이 행렬이라고 할 수 있다. (빈 칸들은 모두 0이다.)

 

• 예시 2) 2가지의 상태(코카콜라 구매/펩시 구매) 만으로 압축해서 보자. 이번엔 예시 1과 달리 비교적 간단하면서 특이한 특징이 하나 생긴다. 각 행(row)과 각 열(column)의 합이 모두 1이 된다는 것이 그 특징이다. 이러한 특징이 어떤 영향을 미치는 지 살펴보자.

n 주 후에 코카콜라를 구매하는 인구 수를 coca(n), 펩시콜라를 구매하는 인구를 pepsi(n)이라고 하면, 이번 주에 코카콜라를 사마시는 인구가 10억명이고 이번주에 펩시콜라를 사 마신 인구가 8억명이라고 하면, 

• coca(1) = 0.8coca(0) + 0.3pepsi(0)
• pepsi(1) = 0.2coca(0) + 0.7pepsi(0)

이고 이를 행렬으로 표현하면 다음과 같다.

만약 이때 n이 무한정 커져서(아주 먼 미래에) 어떤 결과가 나타날지를 보고 싶다면?

n이 점차 10, 50 순으로 계속 커진다고 할 때 어떤 결과가 나타날지 나타내보면, 점차 하나의 값으로 수렴하는 것을 볼 수 있다. 이것은 행과 열의 합이 모두 1인 상태 변이 행렬을 가진 경우에만 해당되는 경우인데, 이 경우 현재의 초기값을 안다면 먼 미래의 값이 수렴하기 때문에 예측하기 쉬운 상태가 된다.

• MDP (Markov Decision Process, 마르코프 의사 결정 과정)

: 결론적으로 마르코프 특성을 기반으로, 환경과의 상호작용(결정 + 보상)을 포함하는 개념인 MDP를 요약하면 다음과 같은 모식도로 나타낼 수 있다.

1. 상태 : state
2. 모델 : model(전이 모델)
3. 행동 : action : 현재 상태에서 가능한 모든 결정들
4. 보상 : reward : 어떤 행동에 대한 값 , R(S,a,S’)
5. 정책 : 마르코프 결정 과정의 해답, π(s)- 최적 정책 : π* (기댓값을 최대로 만드는 정책)

 

---

Reference

https://inst.eecs.berkeley.edu/~cs188/sp22/

https://www.edwith.org/move37/lecture/59775

https://youtu.be/JMpslE8GtCo

https://youtu.be/aAkFtRxeP7c

http://hunkim.github.io/ml/RL/rl03.pdf