고정 헤더 영역
상세 컨텐츠
본문
Q-Table (큐테이블)은 state와 action이 주어지면 사용자가 취할 수 있는 최대값은 얼마라고 나왔다.

지금까지 큐테이블을 사용해왔지만 이는 한계점이 존재한다.
실생활의 더 어려운 예제에 적용해보면 위와 같은 문제에 대해서
표현할 수 있는 수가 상당히 커지기에 한계가 존재한다.
이를 극복하고자 Q-network이 등장하게 된 것이다.

신경망을 이용해 큐테이블에 근사하는 Q-network이다.
이 신경망은 input으로 어떤 state를 받고 output으로 모든 가능한 action의 큐값이 나온다.

이렇게 신경망을 구축한 뒤 큐테이블에서 큐값을 업데이트한 것처럼 신경망도 업데이트를 시켜줘야한다.
이때 이 신경망들의 weights를 W라고 하고 input state를 s라고 하면 output state를 Ws라고 표현할 수 있다.
이 결과 값은 모든 가능한 action의 큐값으로 신경망이 예측한 큐값인 것이다.
이 때, 우리는 Ws가 우리가 원하는 optimal한 Q값을 만들어 낼 수 있도록 해야할 것이다.
이때 optimal Q값을 정답 즉, 라벨로 봤을때 linear regression 문제와 같다고 할 수 있다.
(linear regression은 Wx와 y의 차이가 최소화되도록 만드는 것이 목표였다.)

위 슬라이드에서 이 신경망의 loss function을 같은 원리로 위와 같이 표현할 수 있다.
이 때 y는 label이자 optimal Q이다.

좀더 수학적으로 포멀하게 접근해보자.
Ws는 큐에 대한 예측값이므로 Q^(큐햇)이라고 표현한다.
조건부확률로 표현되어 있는 식에서 s는 state, a는 action, theta는 weight이다.
즉, theta에 의해서 s와 a값이 달라진다.
이때 예측값 Q^과 optimal Q인 Q*이 최대한 같아지게 만드는 것이 우리의 목표이다.
위 두 값의 차이의 제곱을 최소화하는 theta 즉, weight를 구하는 것이 학습의 목표이자 방법인 것이다.
(이는 linear regression과 같은 방법이다.)

위 슬라이드는 전체적인 큐러닝 알고리즘이다.
먼저, 초기의 weight을 랜덤하게 준다.
그리고 에피소드를 M번 루프로 돌게되는데 각 에피소드마다 처음 얻는 state에 전처리를 거친다.
(파이라는 기호는 전처리한다는 뜻이다.)
그런 다음 state에서 어떤 액션을 할 것인지 선택하게 되는데
E-greedy 방법으로 action을 선택하거나, 현재 알고있는 신경망에서의 가장 좋은 action 하나를 선택한다.
그리고 action을 실행하게 되면 환경에서 state와 reward를 돌려주는데 그것을 가지고 신경망 학습을 시킨다.
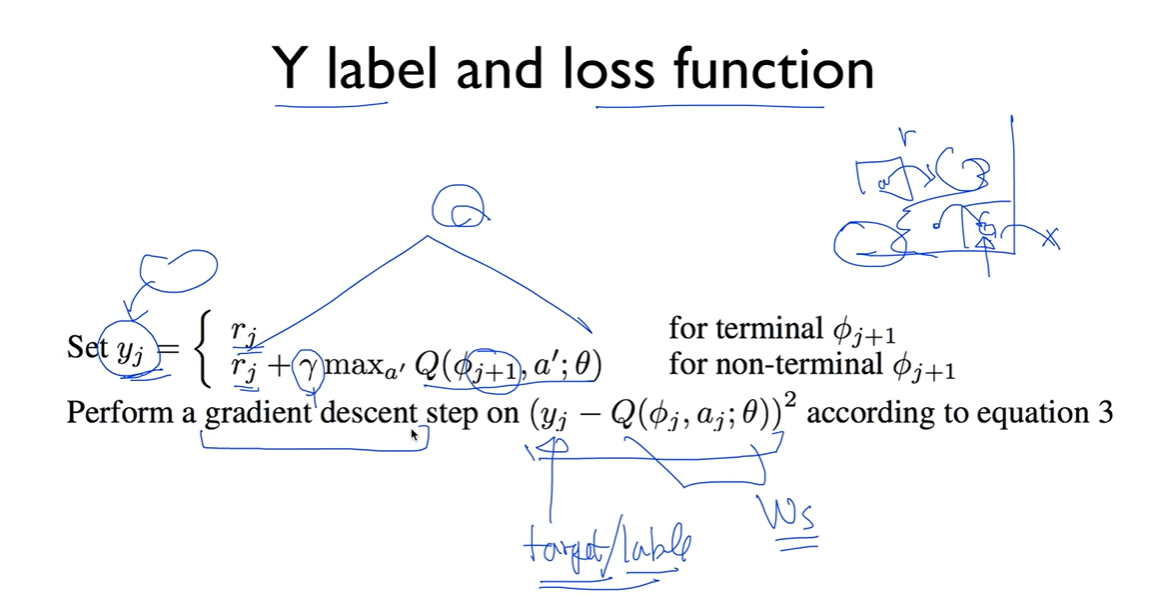
이 때 label인 y를 표현하는 방식은 두 개이다.
만약 다음 state가 terminal state(목표지점)이라면 다음 큐값이 없기 때문에 그냥 거기서 얻은 reward를 y로 설정한다.
만약 terminal state가 아니라면 discount factor를 적용한 Q값과 reward를 더해 y로 설정한다.
그리고 설정한 y값과 이번에 네트워크에서 얻는 Q값의 차이를 계속 좁혀 나가는 gradient descent로 학습시킨다.
위 과정이 네트워크를 학습시키는 핵심 알고리즘이라고 할 수 있다.

지난번에 Deterministic과 Stochastic을 나눠서 계산했는데
Deterministic에서는

이 것이 Q가 되었다.
그러나
Stochastic에서는 위 값을 그대로 넣으면 학습이 되지 않았다.
조금씩 증가시키는 경향을 유지시키고

위와 같은 식의 값으로 설정하였다.
여기서 뉴럴네트워크의 경우를 살펴보면 non-terminal state일 때
y 즉, target 설정을 deterministic할 때의 Q로 지정한 식으로 하였다.
그렇다면 왜 뉴럴네트워크에서 target 설정을 stochastic한 식을 쓰지 않고 deterministic의 식을 사용하는가?
그 이유는 어차피 신경망(네트워크)에서는 조금조금씩 학습되기 때문에
이 식으로 쓰나 저 식으로 쓰나 크게 차이가 없어서 더 간단한 식을 사용하는 것이라고 한다.

그렇다면 과연 이러한 신경망에서도 Q테이블처럼 동일하게 Q값은 수렴할까?
신경망에서는 Q테이블과 다르게 수렴하지 않는다. 분산된다. 즉, 학습이 잘 되지 않는다.
그 이유는
첫번째, 각 샘플들간의 상관관계
두번째, target이 유동적이기 때문이라고 한다.
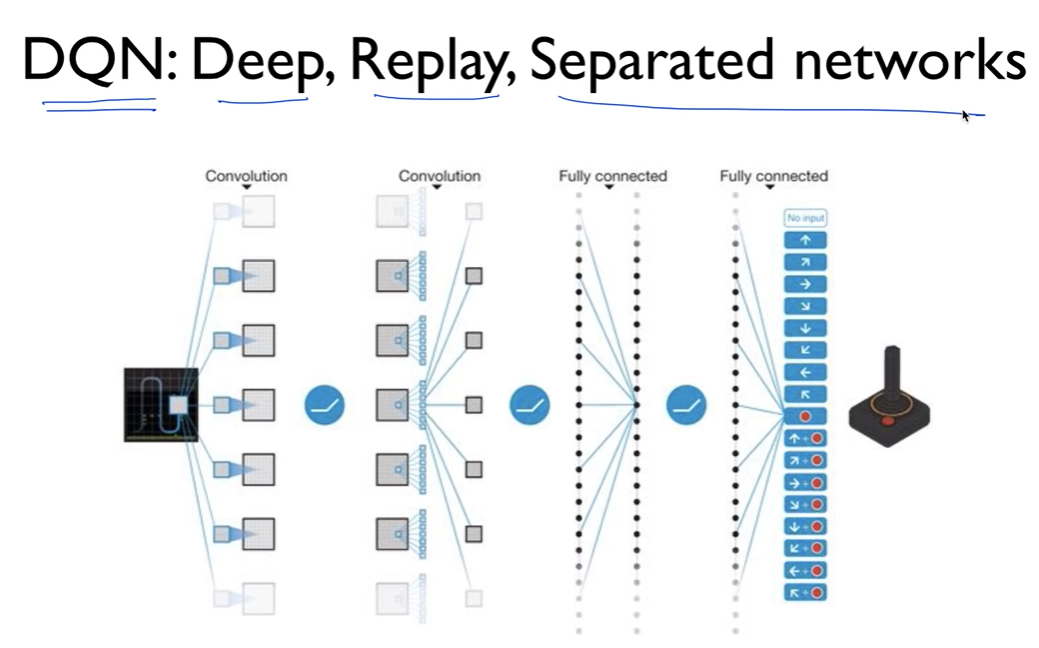
이를 해결한 것이 바로 딥마인드팀의 DQN 알고리즘이다.
세가지로 문제를 해결하였는데
Deep, Replay, Separated networks 깊고 반복하고 네트워크를 분산하였다.
이에 대한 내용은 DQN 강의에서 살펴본다.
'심화 스터디 > 강화학습' 카테고리의 다른 글
| [강화학습 스터디] Introduction to Reinforcement Learning (0) | 2022.04.04 |
|---|---|
| [강화학습 스터디] Q-learning on Nondeterministic Worlds (0) | 2022.03.31 |
| [강화학습] 랜덤탐색 / 칼만필터 (0) | 2022.03.31 |
| [강화학습 스터디] Monte Carlo Methods (0) | 2022.03.24 |
| [강화학습 스터디] Q-learning(table) (0) | 2022.03.24 |





댓글 영역