고정 헤더 영역
상세 컨텐츠
본문
<Markov Decision Process>
- 보상을 최대화하기 위해 주어진 상태에서 최상의 조치를 취함
- 환경은 완전히 관측 가능해야 함
- 마르코프 변수 중 하나라도 모른다면 동적 계획법은 사용할 수 없음
(전이 모델 모름 -> 행동을 취하기 전에 어떤 일이 일어날 지 모름)
(보상 함수 없음 -> 미리 에이전트가 얻을 수 있는 보상 알 수 없음) - 몬테카를로 방법을 사용해야 함
<몬테카를로 방법>
: 반복적인 무작위 샘플링을 통해 수치적 결과를 얻는 다양한 알고리즘
<장점>
- 미리 정의된 전이 함수나 보상 함수가 없어도 환경과의 상호작용을 통해 직접적으로 최적의 행동을 학습할 수 있음
- 전체 상태 중 몇 개에만 집중하기 때문에 쉽고 계산하는 데 효율적임
- 시뮬레이션에 적용할 수 있음
<비교>
<동적 계획법>
- 무차별 대입법
- 구하고자 하는 값이 수렴할 때까지 가능한 모든 상태를 여러 번 순환
- 무수히 많은 행동과 상태가 있는 복잡한 게임에는 실용적이지 않음
<몬테카를로 방법>
- 복잡한 게임에서 최적 정책을 찾는데 훨씬 효율적
- ex)알파고 제로
- 모든 가능성을 시도하는 것이 불가능하거나 실용적이지 않을 때 무작위한 행동을 하거나 이상적으로 지능적인 전략을 세워 가장 시도해보기 좋은 행동을 예측
- 상태의 정확한 가치를 계산하기 보다는 현재 정책을 바탕으로 기대 가치를 계산
<Q러닝>
- Q = Quality
- 상태 s에서 행동 a를 취했을 때 품질이 장기적으로 할인된 보상
<가치함수>
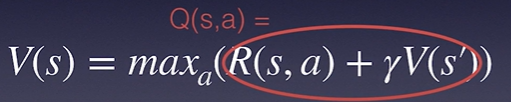
보상은 단기적인 이득만 나타내기 때문에, 각 행동이 얼마나 가치있는지 판단하기 위해 예측한 누적 보상 값
<정책함수>
![]()
에이전트가 판단하는 방식
<비교>
- 벨만 방정식: 게임에 대한 완벽한 지식 요구
- 몬테카를로: 완벽한 값X, 추정치 다룸
- 정확한 가치 추정 > 더 나은 정책 > 더 나은 가치 추정 > ...
<Returns (G)>
- return: 즉각적인 action에 대한 보상 + 현재의 정책을 적용했을 때 얻을 미래의 할인된 보상

- 역순으로 계산하여 추정 값을 얻음
< Returns를 계산하기 위한 알고리즘>
1. G를 0으로 초기화
2. states and returns(상태와 보상)라는 빈 목록 만듦
3. 상태와 보상 목록을 역방향으로 반복
4. (s, G): 현재 상태와 바로 이전의 G값을 상태와 보상 목록에 추가
5. 새로운 G를 보상 + gamma*G로 설정

6. 모든 작업이 완료되면 원래 순서대로 되돌려 검토
<엡실론 그리디>
- 지금까지 알고 있는 정책 활용 + 새로운 조치 모색
- ε: 하이퍼파라미터, 에이전트가 정책을 따르는 대신 임의의 행동을 선택할 확률
- 0과 1사이의 난수 p생성
- p가 1-ε보다 작으면 정책에 정의된 행동을 실행
- 아니면 임의의 행동을 취함
<탐색과 이용>
- 일반적으로 탐색(exploration)과 이용(exploit) 사이의 균형을 찾을 때 가장 높은 보상을 얻음
- 엡실론ε: 무작위한 행동을 취하는 확률
- 에이전트에서 행동을 변경하려면 앱실론 ε의 값을 조절해야 함
- ε를 증가시키는 탐욕 전략을 ε-greedy, 감소시키는 전략을 greedy라고 부른다
- greedy 전략 = 에이전트가 보상에 대해 이미 얻은 지식을 이용할 수 있도록 장려
- ε-greedy 전략 = 에이전트가 무작위적인 행동을 취할 확률을 높여 새로운 보상을 위해 탐색하는 전략을 장려
'심화 스터디 > 강화학습' 카테고리의 다른 글
| [강화학습 스터디] Introduction to Reinforcement Learning (0) | 2022.04.04 |
|---|---|
| [강화학습 스터디] Q-learning on Nondeterministic Worlds (0) | 2022.03.31 |
| [강화학습] 랜덤탐색 / 칼만필터 (0) | 2022.03.31 |
| [강화학습 스터디] Q-network (0) | 2022.03.31 |
| [강화학습 스터디] Q-learning(table) (0) | 2022.03.24 |





댓글 영역