[Practical Statistics for Data Scientists] A팀: Evaluating Classification Models
Confusion Matrix
분류 모델을 평가하기 위한 가장 기본적인 방법은 confusion matrix를 구하는 것이다.
Confusion matrix는 예측값과 실제값을 비교하기 위하여 생성되는 표이다. 해당 표를 통해서 훈련된 모델이 진행한 prediction이 실제 response와 일치하는지의 여부를 쉽게 파악할 수 있다.
예를 들어 y가 {0,1}인 이진 분류기가 있다고 가정하자. Confusion matrix는 다음과 같은 방법으로 그릴 수 있다.
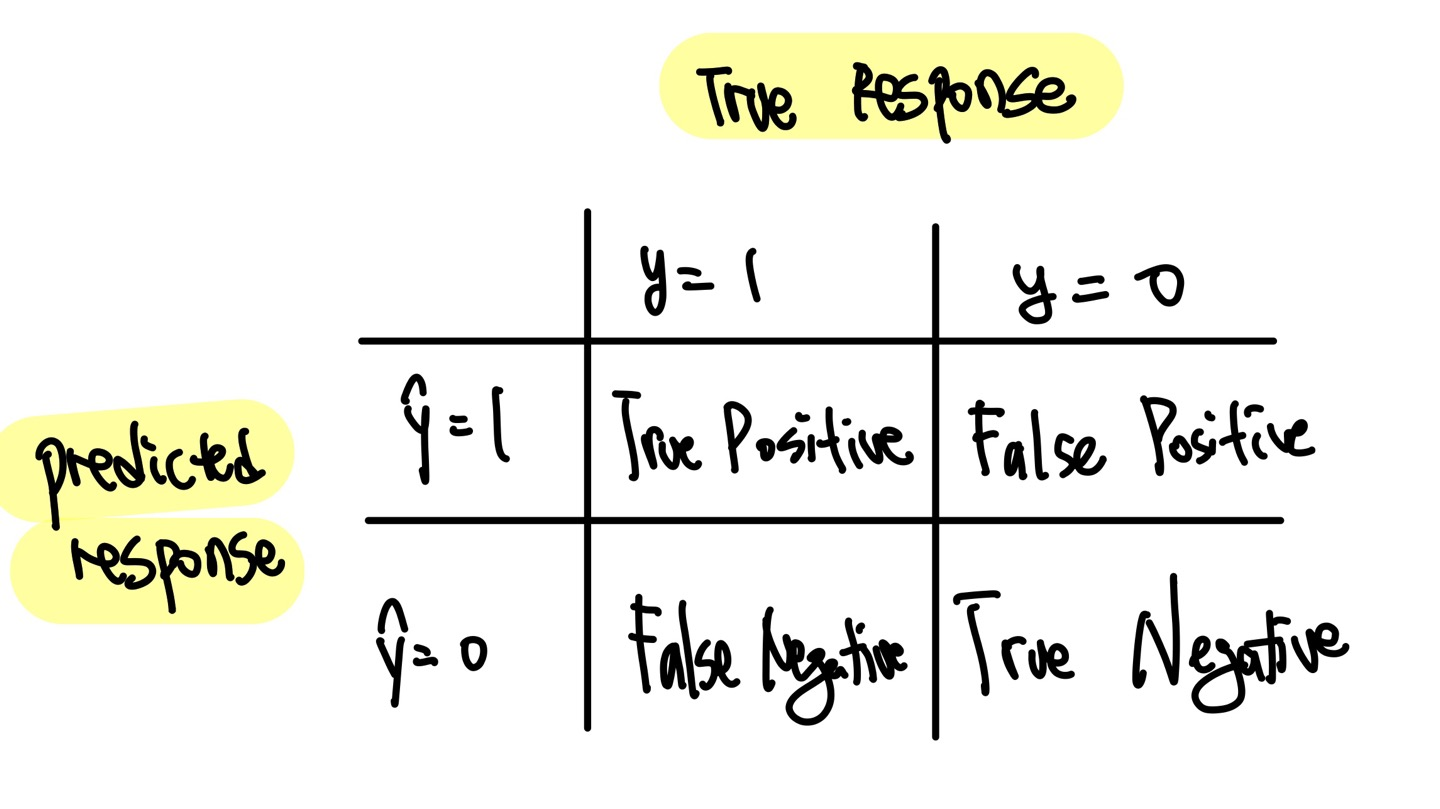
Confusion Matrix의 지표들
Confusion Matrix에는 다양한 지표들이 있다. 각각의 지표들을 알아보자.
Accuracy
정확도라고 하며, confusion matrix에서 구할 수 있는 가장 기본적인 지표이다. Accuracy를 나타내는 공식은 (TP + TN) / (TP + TN + FP + FN)이며, 올바르게 예측한 값의 비율을 구하는 식이다.
Sensitivity(Recall)
민감도라고 하며, 실제로 1인 값 중에서 모델이 1이라고 예측한 것의 비율을 나타낸다. Sensitivity를 나타내는 공식은 TP/(TP + FN) 이다.
Recall은 실제로 1인 데이터를 0으로 잘못 분류했을 때 생기는 손실이 커지는 것을 방지하기 위하여 만들어진 지표이다. 예를 들어서 병원에서 암인 환자를 암이 아니라고 판명하는 것을 방지해야할 때 sensitivity가 자주 쓰인다.
Specificity
특이도라고 하며,실제로 0인 값 중에서 모델이 0이라고 예측한 것의 비율을 나타낸다. Sensitivity를 나타내는 공식은 TN/(TN + FP)이다.
Precision
정밀도라고 하며, 모델이 1이라고 예측한 것 중에서 실제로 1인 값의 비율을 나타낸다. Precision을 나타내는 공식은 TP/(TP + FP) 이다.
ROC Curve
ROC는 "Receiver Operating Characterisitics'의 약자이며, ROC Curve는 모든 임계값에서 분류의 성능을 나타내는 지표이다. X축에는 (1-specificity) 가 들어가며, Y축에는 sensitivity가 들어간다. 이를 달리 표현하면 X축은 FPR(False Positive Rate)을 나타내는 것이고 Y축은 TPR(True Positive Rate)을 나타내는 것이며, ROC Curve는 FPR과 TPR의 관계를 나타내는 곡선이다. 아래는 필자가 22-1학기 KUBIG 프로젝트에서 사용하였던 ROC CURVE의 예시이다. (빨간색 실선)

FPR, TPR모두 0과 1 사이의 값을 가지며, 회색 점선으로 ROC curve가 나타나면 분류를 제대로 못했다는 것이다. (분류가 무작위로 되었다는 뜻과 동일).그러므로 빨간 실선의 아래에 있는 네모의 넓이를 AUC(Area Under the Curve)라고 하며, 최대 1의 값을 가질 수 있다. 즉, 완벽한 분류를 한다는 뜻이다.
Lift
1과0(참과 거짓)으로 분류를 한다고 했을 때, cut-off probability를 0.5로 두고 하는 경향이 있다. 그러나 최적의 cut-off probability가 0.5가 아닐 수도 있는데, 이때 lift의 개념을 사용하여 최적의 cut-off probability를 구할 수 있다.
Lift는 개별 데이터들이 특정한 분위(분포) 내에서 목표범주(ex: 참, 1)에 들어가는 비율이다.
Lift를 구하는 방법은 다음과 같다.
1. 각 관측치에 대한 예측확률을 내림순으로 정렬한다.
2. 데이터를 n개의 구간으로 나누어서 그때의 반응률을 살펴본다. (주로 10개의 decile을 사용)
3. 각각의 반응률을 기본 반응률로 나누어주어 향상도를 구한다.
예를 들어 1800명 중 275명의 환자가 A라는 질병에 걸렸다고 가정을 하자. 이때 1000개의 데이터 각각에 대해서 A 질병에 걸릴 확률을 내림차순으로 정렬하고, 10개의 구간으로 나누어서 그때의 반응률을 살펴본다고 하자. 그렇다면 다음과 같은 표를 만들 수 있다.
*기본 반응률 = 275/1800 = 0.153
| Decile | 발병 빈도 | 반응률 | 향상도 |
| 1 | 145 | 145/275 = 0.527 | 0.527/0.153 = 1.92 |
| 2 | 53 | 53/275 = 0.193 | 0.193 / 0.153 = 1.26 |
| 3 | 40 | 40/275 = 0.145 | 0.145 / 0.153 = 0.95 |
| 4 | 13 | 13/275 = 0.047 | 0.047 / 0.153 = 0.31 |
| 5 | 10 | 10/275 = 0.036 | 0.036 / 0.153 = 0.24 |
| 6 | 6 | 6/275 = 0.022 | 0.022 / 0.153 = 0.14 |
| 7 | 5 | 5/275 = 0.018 | 0.018 / 0.153 = 0.12 |
| 8 | 2 | 2/275 = 0.007 | 0.007 / 0.153 =0.05 |
| 9 | 1 | 1/275 = 0.004 | 0.004 / 0.153 = 0.03 |
| 10 | 0 | 0/275 = 0 | 0 / 0.153= 0 |
앞서 나온 향상도를 그래프로 그리면 빨간색 선과 같은 그림을 확인할 수 있다. 검은색 선은 분류가 제대로 안되었을 때 나오게 되는 그래프이며(병이 있는 환자들이 무작위로 섞여있다), 최적의 선은 파란색 선일 것이다. 그러므로 다양한 cut-off probability로 다양한 향상도 그래프를 그렸을 때, 파란색 선과 가장 유사한 향상도 그래프를 가진 모델이 최적의 모델일 것이다.

향상도 그래프는 누적 향상도 그래프로도 표현할 수 있다.