[Practical Statistics for Data Scientists] A팀 : Interpreting the Regression Equation
# Interpreting the Regression Equation
- 회귀분석에서, 종속변수를 예측하는 것뿐만 아니라 회귀식을 보고 변수들 간의 관계를 해석하는 것도 중요하다.
# Correlated Predictors
- 다중회귀에서, 예측변수들 간에 상관관계가 있는 경우가 많다.

- Bedrooms의 계수가 음수 : 침실의 개수가 증가할수록 주택 가격이 하락
- 침실의 개수(Bedrooms)와 집의 크기(SqFtTotLiving)간의 상관관계 존재
-> SqFtTotLiving 변수가 회귀식에 포함되어 있기 때문에, Bedrooms는 집의 크기를 고정했을 때 침실 개수의 영향 을 나타냄.
-> 같은 크기의 집에 침실이 많으면 Undesirable.
* 상관관계가 있는 예측변수들을 사용하면 coef 의미 해석에 방해가 될 수 있다.
-> (SqFtTotLiving,SqFtFinBasement,Bathrooms)를 제거한 모델에서는 Bedrooms의 계수가 양수.

# Multicolinearity
- 예측변수들 간의 상관 정도가 높아 회귀분석에 부정적 영향을 미치는 현상
- 예측변수들 간의 극단적인 상관성 <-> 한 예측변수를 다른 변수의 선형결합으로 표현 가능 (완전한 상관관계 경우)
* 다중공선성은 다음 경우에 주로 발생
- 똑같은 변수를 실수로 여러번 넣은 경우
- P개 범주의 변수에 대해 P-1 개 의 더미변수가 아닌 P개의 더미변수를 생성한 경우

- 두 변수가 거의 완전한 상관관계를 갖는 경우
# Confounding Variables
- 회귀식에 포함되어있지 않지만 중요한 영향을 갖고있어 잘못된 결론을 내리도록 하는 변수
- 주택 가격 데이터 회귀 예시 : SqFtlot(토지 규모), Bathrooms, Bedrooms의 계수가 모두 음수

- 중요한 예측변수이지만 회귀식에서 독립 누락된 Location을 회귀식에 포함
-> 우편변호를 5개의 범주로 나누어 다시 회귀(ZipGroup2~ZipGroup5 생성, ZiPGroup1이 Baseline Model)
-> Bedrooms를 제외한 나머지 2개 계수가 양수로 바뀜.

# Interactions & Main Effects
- Main effect : (하나의) 예측변수가 종속변수에 미치는 효과
y ~ x1 + x2 + x3 + ....
- Interaction : 둘 이상의 예측변수의 조합이 종속변수에 미치는 효과
y ~ x1 + x2 + x1*x2 + x3 + ....
- 주택 가격 데이터 회귀 예시 : 지역(ZipGroup)을 포함하는 모델에서, 잘 사는 지역일수록 주택 크기가 가격에 주는 영향이 클 것이라고 예상
-> 주택 크기 * ZipGroup5(가장 잘 사는 지역) 의 계수가 가장 큰 것을 볼 수 있음.

# Regression Diagnostics
- 앞에서 언급한 내용들을 종합적으로 고려해 모델의 적합성을 평가한다.
- 잔차분석을 기본으로 한다.
# Outlier
- 데이터에서 (Q1 - 1.5*IQR, Q3 + 1.5*IQR) 의 범위를 넘는 값을 Outlier라 한다. (IQR = Q3- Q1)
- 회귀식에서는 예측치와 멀리 떨어진 관측치를 Outlier라 함.
-> 표준화잔차의 절대값 클수록 멀리 떨어진 것
# Influential Values
- Influential Observation : 회귀에서 제외되었을 때 큰 변화를 가져오는 값
- influential obs라고 해서 표준화잔차가 큰 것은(outlier인 것은) 아님
-> 높은 leverage를 갖는다고 표현. (leverage : 실제 y값이 예측값에 미치는 영향을 나타낸 값)
- ex) 우측 상단 점을 포함시킨 회귀식과 제외한 회귀식이 큰 차이가 있다.

# 단일 obs의 영향력을 결정하는 추가적인 방법
- Hat value : h_ii > 2(P+1)/n 이면 높은 레버리지를 갖는다고 말할 수 있다.

- Cook's distance : 표준화잔차와 레버리지를 모두 고려한 지표
- 통상적으로 4/(n-p-1) 보다 크면 해당 높은 레버리지를 갖는다고 말할 수 있다.
- ex) 버블차트 :
-> x축 : Hat value, y축 : 표준화잔차, 원의 크기 : 쿡의 거리, 색칠 여부 : 쿡의 거리가 0.08보다 큰 값.

- 통계적 추론을 위한 세 가지 가정 : 데이터사이언스에서도 모델의 유효성과 관련있으니 주목할만함.
- 잔차에 대해 세 가지 가정을 살펴본다.
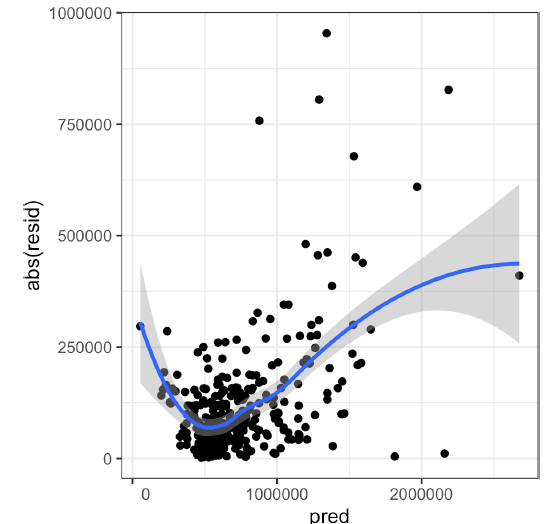
# 정규성
- 주택 가격 회귀식모델에서는 잔차의 분포가 정규분포보다 평균에 집중(꼬리가 길다)

# 독립성
- 주로 시계열 데이터에서, 오차가 독립적이라는 가정을 확인하기도 한다.
-> 더빈-왓슨 통계량 : 잔차의 독립성을 확인할 때 사용, 0~4 사이 값을 가지며 2에 가까울수록
자기상관이 없고 0,4에 가까울수록 자기상관이 심하다.(t-1시점과t시점 잔차의 상관을 측정)
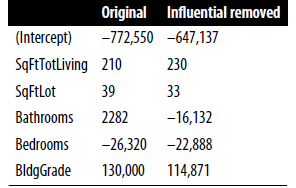
# 편잔차플롯 & 비선형성

<- 하나의 예측변수와 응답변수 사이의 관계 표현
-> 1000~2000 제곱피트의 집 : 가격을 원래보다 낮게 추정
2000~3000 제곱피트의 집 : 가격을 높게 추정
-> SqFtTotliving에 대해 선형항이 아닌 비선형항을 고려할 수 있음.