[강화학습 스터디] Policy Based Methods

심화 스터디/강화학습

[강화학습 스터디] Policy Based Methods

남르미누 2022. 5. 12. 02:12

작성자 : 남정재

1. 메타러닝

메타러닝

높은 단계의 AI가 낮은 단계의 AI 혹은 그들 여러개를 최적화하는 것

(강의 URL) https://www.youtube.com/watch?v=2z0ofe2lpz4&feature=emb_imp_woyt

'메타' : 한 차원 위의 개념적 용어로 대상의 전반적인 특성을 반영

메타 러닝은

데이터의 패턴을 정해진 프로세스로 학습하는 것이 아니라,

데이터의 특성에 맞춰서 모델 네트워크의 구조를 변화시키면서 학습하는 것

즉, 배우는 방법을 배우는 것(Learning to learn).

메타 러닝은 범위 : 굉장히 광범위

최근에는 하이퍼파라미터 최적화, 자동 신경망 네트워크 설계 등으로 가장 많이 활용됨

기존의 딥러닝 모델은 일반적으로 데이터가 많은 경우 효과적임

BUT, 사람은 배경 지식 및 유연한 사고력으로 적은 몇장의 사진만으로도 구분할 수 있음

메타 러닝은 인간의 유연한 사고력을 모델링을 통해 구현하고자 합니다.

>> 즉, 적은 데이터로도 인간의 사고력을 모델링 구현 가능

(예시)

지도 학습 vs 메타러닝 비교

수달을 처음 본 로봇들은 "이 동물은 뭐야?"라고 묻습니다.

지도 학습 로봇에게는 각기 다른 수달의 사진을 1000장을 보여줍니다.

그 결과 아래 카드리스트에서 수달을 찾을 수 있게 되었습니다.

메타 러닝 로봇에게는 카드를 먼저 보여줬습니다.

메타 러닝 로봇은 따로 사진을 학습하지 않아도 카드리스트에서 수달을 찾아낼 수 있었습니다.

퓨샷 러닝(Few shot Learning)

(기존의 문제점)

일반적으로 딥러닝 모델을 제대로 훈련시키기 위해 대용량의 데이터가 필요함

거대한 데이터셋을 구축하기 위해서는 그만큼의 막대한 비용과 시간이 소모...

>> 전이학습의 등장

전이 학습(Transfer Learning)

: 큰 데이터로 학습한 가중치의 일부를 새로운 데이터에 맞춰서 학습하는 것

BUT, 전이 학습의 문제점

>> 새로운 문제에 적용하기 위해서 많은 수의 데이터와 레이블링이 필요함

& 어떤 문제의 사전 학습 모델이 해당 데이터에 적합한 지 판단하기 어려움

>> 퓨샷 러닝의 등장

퓨샷 러닝(Few Shot Learning)

: 소수의 예제(Few)만 있어도 성능이 우수한 모델링이 가능

적은 데이터를 효율적으로 학습하는 문제(Few shot task)를 위해 탄생

cf.) 메타러닝은 퓨샷러닝을 해결하기 위한 알고리즘

(퓨샷 러닝에서의 데이터셋 2가지) : 서포트 셋(Support Set), 쿼리 셋(Query set)

서포트 셋 : 데이터 셋을 학습에 사용하는 데이터

쿼리 셋 : 데이터 셋을 테스트에 사용하는 데이터

퓨샷 러닝 태스크(Few Shot Learning Task)를 "N-way K-shot"이라고 함

(카테고리 개수만큼의 방법수, 카테고리당 데이터수)

n : 카테고리의 개수

k : 카테고리당 이미지의 수

다람쥐, 토끼, 햄스터, 수달의 카테고리가 4개 있고 각각 2장씩 있으면?

>> 4-way 2-shot

성능은 n에 반비례, k에 비례

과목의 수가 많을수록 시험 성적이 낮고

과목당 문제집을 많이 풀수록 높아지는 것

Key Idea

(메타 러닝 및 퓨샷 러닝의 대표적 접근 방법)

거리 학습 기반(Metric Based Learning) : '효율적 거리 측정' 학습이 핵심

모델 기반 학습 방식(Model-Based Approach) : '메모리를 이용한 순환 신경망'이 핵심

최적화 학습 방식(Optimizer Learning) : '모델 파라미터 최적화'이 핵심

거리 학습 기반 (Metric Based Learning)

서포트 셋과 쿼리 셋 간의 거리(유사도)를 측정하는 방식

(ex) 샴 네트워크(Siamese Neural Network)

주어진 서포트 데이터를 특성 공간(Feature Space)에 나타내서 특징 추출

같은 클래스면 거리를 가깝게, 다른 클래스면 멀게 하는 방식 >> 데이터 분류

쿼리 데이터(test data)를 유클리디안 거리가 가까운 서포트 데이터(train data)의 클래스로 예측하는 방식

모델 기반 학습 방식 (Model based learning)

적은 수의 학습 단계로도 모델의 파라미터를 효율적으로 학습할 수 있는 방식

(+ 모델에 별도의 메모리를 두어 학습 속도를 조절함)

(ex) MANN(Memory-Augmented Neural Networks) 알고리즘

외부 메모리 보유

>> 과거 데이터를 외부 메모리에 저장함으로써 효율적으로 문제를 해결하는 방법을 습득함

>> 새로운 정보를 빠르게 인코딩하고, 몇 개의 샘플만 가지고도 새로운 태스크에 적용할 수 있도록 설계됨

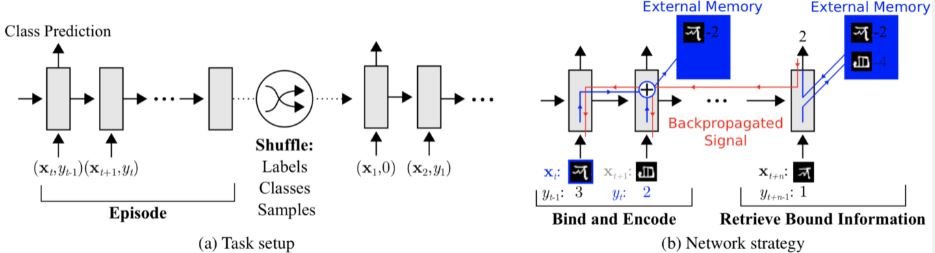
최적화 학습 방식(Optimizer learning)

퓨삿 태스크를 파라미터 최적화 문제로 생각하는 방식

일반적으로 딥러닝 모델은 기울기의 역전파를 통해 학습을 진행함

BUT, 기울기 기반 최적화 기법은 퓨샷 태스크가 아닌 큰 스케일의 데이터를 위해 설계가 되었음

So, 최적화 기반 메타 러닝은 적은 수의 샘플에 대한 최적화 기법에 대해 다룸

(ex) MAML(Model-Agnostic Meta-Learning) 알고리즘

실선 : 각 태스크에서 계산했던 그래디언트를 합산하여 모델을 업데이트하는 것을 의미

즉, 1, 2, 3의 데이터에서 학습된 그래디언트 정보를 기반으로 전반적인(전체적인) 파라미터를 업데이트함

점선 : 공통 파라미터로부터 다시 모델이 각 데이터를 학습하면서 세부 파라미터를 업데이트함

이런 과정을 최적의 파라미터를 찾을 때까지 반복하여 모델의 파라미터 최적화하는 방식

마무리

퓨샷 러닝은 기존 딥러닝(많은 데이터 필요, 라벨링 작업 등)에 비교적 몇 개의 예제만 주어져도 충분함!

많은 수의 학습 데이터를 확보하기 어려운 경우에도 우수한 성능을 달성할 수 있음!

메타 러닝은 최근 멀티태스크 러닝(Multi-task Learing)과 함께 적은 데이터 문제를 해결할 수 있는 아주 효과적인 방법론 중 하나로 부상함!

(참고자료) https://bigwaveai.tistory.com/18

메타 러닝(Few Shot Task) - 적은 데이터로도 성능은 강력하게!

안녕하세요! 빅웨이브에이아이의 박정환입니다. 지난 포스팅 글은 딥러닝에 대해서 쉽고 간단하게 알아보았었는데요 ! <혹시나 못보신 분들을 위한 링크 딥러닝,그거 어떻게 하는건데? > 이

bigwaveai.tistory.com

2. 정책 검색 알고리즘

* 행동 검색 vs 정책 검색

- 행동 검색 알고리즘

: 각 상태에 대한 행동(혹은 가치 함수 근사를 다룰 때는 특성 벡터)을 최대화하여 최적 정책 찾음

(ex) Q-러닝, Fitted-Q, LSTD-Q

- 정책 검색 알고리즘

: 정책 공간을 직접 탐색함 (여기서 정책 검색은 마르코프 결정 과정을 해결하기 위해 정책을 직접 학습하는 방법을 말함)

(ex) 정책 경사 : 가치 함수를 학습하고 이 가치를 사용해 주어진 마르코프 결정 과정을 위한 정책을 학습 - 액터 크리틱 기법(추정한 가치 함수로 정책을 비교하여 분산을 줄인다는 차이점 있음)

(ex) 전역 최적화 알고리즘 - 최적화를 위한 교차 엔트로피 기법과 낙관적 최적화 기법

정책 검색과 정책 반복의 차이점:

정책 검색은 정책 공간에서 최적 정책을 찾습니다.

정책 : S→A이란 상태를 행동에 매핑한 것입니다.

만약 상태와 행동 집합이 유한하다면, 가능한 정책 또한 유한합니다.

따라서 모든 가능한 정책의 집합에서 최적 정책을 탐색할 수 있습니다.

만약 상태-행동 집합이 연속적이라면, 최적 정책은 무한한 차원의 벡터 공간에 존재할 수도 있습니다.

이런 경우, 정책을 매개 변수(w∈W)로 표현하여

매개 변수 공간 W(즉, 유한 차원 벡터 공간의 하위집합 - 예: W⊆ℜM)에서 탐색하는 것이 일반적인 접근법입니다.

위 두 경우 모두, 검색을 최적화 문제로 변환하여 몬테카를로 트리 검색, 교차 엔트로피, 유전 알고리즘, 혹은 힐클라이밍서치와 같은 최적화 알고리즘을 사용하면 보상이 극대화되는 지역 최적점을 얻을 수 있습니다. 정책 경사(즉, 정책 공간에서의 정책 상승법)나 기댓값-최대화(즉, 최적 정책이 최대-우도 문제로 추정되어야 하는 잠재적 확률 변수인 베이지안 학습 구조)와 같은 방법도 있습니다.

요점은 정책 반복과 정책 검색은 배타적인 분류가 아니라는 것입니다.

정책 검색을 최적화 문제로 본다면, 문제의 목적(예, 정책의 특정 함수의 최적화)를 정의하는 것은 매우 중요합니다.

가치 함수는 목적함수가 될만한 좋은 후보입니다.

표본을 사용해 추정(예, 시간차 방법)하면 누적 보상을 평균할 때보다 분산이 더 적기 때문입니다.

이런 관찰 결과를 통해 "액터 크리틱 기법" 이 만들어졌습니다.

크리틱이 현재 정책의 가치를 추정(정책 평가)하고,

액터는 이 값을 사용해 정책 경사(정책 발전)를 적용합니다.

이런 관점에서, 액터 크리틱 기법은

정책 검색 방법(정책 경사를 사용하기 때문에)과 근사 정책 반복 알고리즘(정책 평가와 정책 발전을 하기 때문에)

모두에 속합니다.

같은 개념을 적용하면 "SARSA" 또한 정책 검색 방법으로 볼 수 있습니다.

매 순환 현재 추정된 가치 함수를 바탕으로 탐욕 정책을 사용하여 정책을 조금씩 개선해 나가기 때문입니다.

정책 순환 또한 정책 검색의 한 종류로 볼 수 있습니다.

두 기법 모두 수렴될 때까지 (확률론적으로) 개선되는 정적인 정책들을 제공하기 때문입니다.

반면, 정적인 정책들의 시퀀스를 얻는다는 아이디어는 가치 순환 알고리즘과는 다릅니다.

가치 순환 알고리즘은 추정한 최적 가치 함수의 시퀀스를 제공하기 때문이죠.

그리고 최적값에 수렴해서야 최적 정책(최적값에 대응하는 탐욕 정책)을 알게 됩니다.

다르게 말하면, 가치 순환 방법은 가치 함수 공간에서 탐색하고 이에 부산물로 최적 정책을 얻는 것입니다.

이것은 중요한 포인트입니다.

우리는 가치 함수 공간과 정책 공간에서 탐색하는 것을 구별할 수 있습니다.

첫 번째 경우, 가장 유리한 상태를 많이 방문하기 위해 찾아낸 추정 가치를 통해 얻은 정책들을 바탕으로 탐색합니다.

두 번째 경우, 찾아낸 정책과 연관된 추정 가치 함수를 바탕으로 탐색합니다.

(???)

이를 통해 '가치 함수 공간에서의 최적화' 와 '정책 공간에서의 최적화' 는 쌍정 문제라는 것을 알 수 있습니다.

이 주쌍 관계가 가치 순환 방법이 가치 검색 방법에 속한다는 주장을 뒷받침합니다.

(참고자료)

https://jyoondev.tistory.com/145

강화학습 - (12) 정책 반복

강화학습 정책 향상 강화학습의 궁극적인 목표중 하나인 제어(Control)를 하기 위해서는 정책 향상이 필요하다. 이미 최적 가치를 알고 있고, 탐욕적인 정책을 사용했다고 가정했을 때 벨만 방정

jyoondev.tistory.com

왜 정책 기반 방법을 사용할까요?

정책은 결정론적이거나 확률론적일 수 있습니다.

결정론적인 정책은 상태를 행동으로 매핑하는 정책입니다.

어떤 상태가 주어지면, 함수는 취해야 할 행동을 반환합니다.

결정론적인 정책은 결정론적인 환경에서 사용합니다.

이는 행동이 특정 결과를 결정하는 환경을 말합니다.

불확실성이 없습니다.

예를 들어, 체스 할 때 말을 A2에서 A3로 옮기면 말이 A3로 갈 것을 확신할 수 있습니다.

반면, 확률론적인 정책은 행동에 대한 확률 분포를 반환합니다.

즉, 행동 a(예, 왼쪽으로 이동)를 무조건 행하는 것이 아니라 다른 행동(남쪽으로 갈 확률 30%)을 취할 확률도 있습니다.

확률론적인 정책은 환경이 불확실할 때 사용합니다.

이런 과정을 부분 관찰 가능한 마르코프 결정 과정(POMDP)이라고 부릅니다.

우리는 대부분 확률론적인 정책을 사용할 것입니다.

장점:

정책 기반 방법은 더 좋은 수렴성을 가지고 있습니다.

가치 기반 방법의 문제는 학습 시 큰 기복이 있을 수 있다는 것입니다.

이는 추정된 행동 가치의 작은 변화에도 행동 선택은 크게 변할 수 있기 때문입니다.

반면, 정책 경사에서는 가장 좋은 매개 변수를 찾기 위해 경사를 따라갑니다.

따라서 매 스텝 정책이 부드럽게 갱신되는 것을 볼 수 있습니다.

가장 좋은 매개 변수를 찾기 위해 경사를 따라가기 때문에,

지역 최고점(최악의 경우)이나 전역 최고점(최선의 경우)에 수렴할 것을 보장할 수 있습니다.

정책 경사는 고차원 행동 공간에서 더욱더 효과적입니다.

두 번째 장점은 정책 경사는 고차원 행동 공간이나 연속적인 행동 공간에서 더 효과적이라는 것입니다.

딥 Q-러닝의 문제점은 예측이 주어진 현재 상태에 대해서 각 시간점마다 모든 가능한 행동의 점수(최대 미래 보상 기댓값)를 매긴다는 점입니다.

하지만 만약 가능한 행동이 무한하다면 어떻게 할까요?

예를 들어, 자동주행차는 각 상태에서 (거의) 무한한 가짓수의 행동(바퀴를 15°, 17.2°, 19.4° 회전 ...)을 선택을 할 수 있습니다. 그럼 모든 가능한 행동에 대하여 Q값을 구해야 하게 됩니다!

반면 정책 기반 방법에서는 매개 변수를 직접 조정할 수 있습니다.

따라서, 매 스텝 최고점을 직접 계산(추정)하지 않고 천천히 최고점을 알아갈 수 있습니다.

정책 경사는 확률론적인 정책을 학습할 수 있습니다.

정책 경사의 세 번째 장점은 가치 함수와 달리 확률론적인 정책을 학습할 수 있다는 것입니다.

이는 두 가지 결과를 낳습니다.

첫 번째는 탐색/이용 균형을 구현할 필요가 없다는 것입니다.

확률론적인 정책을 사용하면 에이전트는 같은 행동을 취하지 않고 상태 공간을 탐색할 수 있습니다.

행동에 대한 확률 분포를 반환하기 때문입니다.

따라서, 직접 하드코딩하지 않아도 탐색/이용 균형이 자연스럽게 맞춰집니다.

두 번째는 지각적 에일리어싱(perceptual aliasing) 문제도 사라진다는 것입니다.

지각적 에일리어싱이란 두 상태가 (실제로 똑같거나) 똑같아 보이지만 다른 행동이 필요한 상황을 말합니다.

가치 기반 강화 학습 알고리즘을 사용하면 준-결정론적인 정책을 학습하게 됩니다. ("엡실론 탐욕 전략")

결과적으로, 에이전트는 먼지를 찾기 전에 훨씬 많은 시간을 소비할 수도 있습니다.

반면, 최적 확률론적 정책은 회색 상태에서 무작위로 오른쪽이나 왼쪽으로 가게 할 것입니다.

결과적으로 에이전트는 갇히지 않고 높은 확률로 목표 상태에 도달하게 됩니다.

단점:

정책 경사는 많은 상황에서 전역 최적점이 아닌 지역 최적점에 수렴합니다.

항상 최고점에 도달하려는 딥 Q-러닝과 달리, 정책 경사는 천천히 수렴합니다.

따라서 학습하는 데 더 오랜 시간이 걸릴 수 있습니다.

이제 정책 검색 방법의 두 하위분류와 예시를 보겠습니다.

모델-프리 정책 검색 기법:

정책 경사
우도 경사: REINFORCE [Williams, 1992], PGPE [Rückstiesset al, 2009]
자연 경사 (Natural Gradients): episodic Natural Actor Critic (eNAC), [Peters & Schaal, 2006]
가중 최우도 방법 (Weighted Maximum Likelihood Approaches)
성공-매칭 원리 (Success-Matching Principle) [Kober & Peters, 2006]
정보 이론 기법 (Information Theoretic Methods) [Daniel, Neumann & Peters, 2012]
확장: 맥락/계층적 정책 검색 (Extensions: Contextual and Hierarchical Policy Search)

모델-기반 정책 검색 기법:

탐욕 갱신: PILCO [Deisenroth& Rasmussen, 2011]
유계 갱신 (Bounded Updates): 모델-기반 REPS [Peters at al., 2010], 궤적 최적화에 의한 유도 정책 검색 (Guided Policy Search by Trajectory Optimization) [Levine &Koltun, 2010]

3. 진화 알고리즘

진화 알고리즘이란?

유전학과 진화학에서 영감을 얻어 만들어진 최적화 기법

- 주어진 문제에 대한 해의 후보가 되는 해 집단에서 시작하여 우수한 해들은 남기고 나머지는 제거함

- 그리고 전이 및/또는 교배를 통해 변화를 주면 알고리즘은 새로운 탐색 공간을 탐색함

- (변이를 통해) 새로운 유전자를 형성하지 않으면 제한된 유전자풀로 인해 진화 과정이 침체될 수 있음

어떤 진화 알고리즘이 있을까요?

- 유전 알고리즘

: 어떤 문제를 해결하기 위해 유전체를 숫자(초기에는 이진법)의 문자열로 나타내고 적합성 함수를 사용해 반복적으로 발전해나가는 알고리즘

- 진화 전략

: 실수 벡터를 사용하는 유전 알고리즘

- 유전 프로그래밍

: 프로그램을 생성하기 위해 사용하는 유전 알고리즘

- 신경 진화

: 신경망에 적용하는 유전 프로그래밍

진화 알고리즘의 과정은 어떻게 될까요?

1. 초기화 : 초기해 집단을 생성합니다.

2. 선택 : 적합도 함수를 사용해 각 해를 평가합니다.

3. 유전적 연산 : (‘a’ 혹은 ‘a와 b’)

- 변이: 무작위한 변화로 유전자의 다양성을 늘립니다.

- 교배: 우수한 해 간의 유전자를 교환합니다.

(2와 3을 반복)

4. 종료: 최대 실행 시간이나 성능 한계점에 도달하면 종료합니다.

다른 방법과 비교했을 때 진화 알고리즘은 어떤 장점이 있을까요?

더 큰 탐색 공간을 다룰 수 있습니다
매우 창의적인 접근법입니다
경사가 필요하지 않습니다

진화 알고리즘은 어떤 종류의 문제에 사용하기 좋을까요?

해에 대한 탐색 공간이 매우 큰 문제
경사를 계산할 수 없는 문제
블랙박스 공학: 충분한 정보를 주는 모델이 없는 문제
양자 연산: 반직관적인 양자학 알고리즘의 설계

진화 알고리즘을 어떻게 신경망과 함께 사용할 수 있을까요?

진화 알고리즘을 사용해 가중치를 학습시킬 수 있습니다. (전통적인 신경 진화)
신경 구조 탐색: 최적 신경망 구조를 찾기 위해 사용할 수 있습니다.
신경망을 사용해 특성을 찾고 진화를 사용해 정책을 구합니다.