[분류 예측 스터디] Survial support vector machine
이 글에서는 "An Efficient Training Algorithm for Kernel Survival Support Vector Machines" 논문을 리뷰를 담아 보려고 합니다. Sebastian Polsterl, Nassir Navab, and Amin Katouzian이 작성한 논문입니다. 논문에서 소개하는 모델은 임상분야에서 사용되는 것입니다.
1. 서론
생존분석은 의학 연구에서 사용되는 주된 도구입니다. 이 분야에서 주요 목표는 어떠한 사건이 발생한 시간과 feature 간의 연결고리를 찾는 것입니다. 예를 들어 사건이 생겼을 때 그 사건의 요인을 알아보는 것을 말합니다. 임상연구에서는 환자들은 관찰되고 그 기간들이 기록됩니다. 즉 환자가 어떠한 사건을 겪으면 그 사건에 대한 정확한 시간이 기록되는 것입니다. 그런데 문제는 연구가 끝나게 되었을 때 환자에게 사건을 발생했는지 안 했는지를 모르게 됩니다. 그래서 이를 사건의 시간은 연구 마지막에 'Right censored' 된다고 말합니다.
cf) Right-censored data. Failures are seen only if they occur before a particular time. A unit surviving longer than that time is considered a right-censored observation. Right-censored data are sometimes time-censored or failure-censored. Time censoring means that you perform the study for a specified period of time.
Time - event 데이터에 있어 CoxPH모델이 있는데 이 모델은 covariates에 선형관계를 가져서 약한 예측력을 가지는 단점을 가지고 있습니다. 하지만 Kernel method가 등장하게 되면서 Kernel-based survival models를 제안할 수 있었습니다. 이는 비선형 분석에도 용이하며, 복잡한 data에도 좋은 결과를 보여주는 model입니다. 이는 단순한 피처를 통한 환자 묘사를 넘어서 구조적이고 표현 가능한 형태를 만드는 데에 가능하게 해 주었습니다. 이 논문의 저자는 이 모델에 대한 문제점을 지적하여 새로운 학습 시스템을 제안하고 있습니다. 그 문제점은 두 가지가 있습니다.
1) Rank problem
the model learns to assign samples with shorter survival times a lower rank by considering all possible pairs of samples in the training data.
2) Regression problem
the model learns to directly predict the (log) survival time.
In both cases, the disadvantage is that predictions cannot be easily related to standard quantities in survival analysis, namely survival function and cumulative hazard function. Moreover, they have to retain a copy of the training data to do predictions.
논문의 저자는 최적화 방법에 집중을 했습니다. 기존의 훈련 알고리즘은 많은 시간과 공간이 필요합니다. 최근에 나온 알고르즘인 linear SSVM은 시간과 복잡성을 많이 낮췄습니다. 그러나 저자는 이것을 넘어서 비선형 데이터까지 확장시키려고 했습니다.
2. 본론
## Survial support Vector Machine
SSVM은 RankSVM의 확장 버전으로 right censored survival data에 대한 알고리즘입니다.
Censoring X - all sample used
Censored - some relationship invaild , (앞서 ranking problem에서 다뤘듯이 샘플들 사이에서 뭐가 더 순위가 높이 매겨져야 하는지는 모르는 것입니다 왜냐하면 사건이 일어난 실제 시간을 모르기 때문에)
그래서 이 비교 자체를 다음과 같은 것으로 했습니다.

-> 이 비교는 더 빨리 사건이 나타난 샘플의 시간이 uncensor 이여야 비교가 가능하다
하나의 샘플의 시간보다 다른 하나의 샘플의 시간이 더 낮으면 그 다른 하나의 샘플의 시간이 uncensor된 것
Linear SSVM를 훈련시키는 것은 최적화 문제가 따라옵니다. censor를 하지 않으면 모든 샘플을 다뤄야하기 때문에 최적화 문제에 있어서 해결해야 할 상황입니다. survival time의 part를 censor를 하게 되면 사이즈 자체는 절단되지 않는 기록들에 의존하게 됩니다. 이는 즉 마지막 관찰된 사건의 시간 포인트 이후에 처음 검열된 시간 포인트가 일어나는 것입니다. 모든 중도 절단되지 않는 기록들이 중도 절단된 시간들과 비교가 될 수 있는 것이죠.
p는 O(qen^2)의 순서와 최적화문제에 가수의 수가 샘플들의 수에 이차식입니다. 목적함수에서는 Lagrange dual problem을 해결하면서 minimised 됩니다.
cf) The Lagrangian dual problem is obtained by forming the Lagrangian of a minimization problem by using nonnegative Lagrange multipliers to add the constraints to the objective function, and then solving for the primal variable values that minimize the original objective function
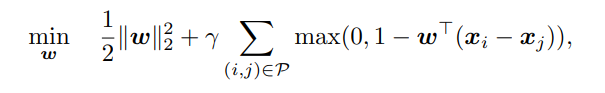

이 접근 자체는 다루기가 힘든 방법입니다. 함수 식 안에 있는 행렬 식 자체는 많은 공간과 시간을 요구하기 때문입니다.
그래서 Van Belle 제안을 했습니다. size of P를 줄이는 것입니다. 그에 해당하는 요소는 짝지어진 짝에서 가장 큰 검열되지않는 샘플이 있는 요소를 가리킵니다.
그러나 다른 문제점이 또 있었습니다.
이전에 저자는 hinge loss를 squared로 바꿔서 truncated Newton optimisation / order statistics tree를 사용하여 복잡한 구조를 만들 필요 없고 그래서 시간과 복잡성을 줄일 수 있게 되었다.
그러나 이 최적화는 linear model에서만 가능했는데 이를 극복하기 위해서 data Kernel PCA 훈련전에 실시하였다.
이를 통해 non linear data도 가능하게 되었다. 그러나 이 접근 방법의 단점도 operation cost 문제가 있었다.
cf) Truncated Newton method - Wikipedia - > truncated Newton method 내용
cf) Hinge Loss
The hinge loss is a specific type of cost function that incorporates a margin or distance from the classification boundary into the cost calculation. Even if new observations are classified correctly, they can incur a penalty if the margin from the decision boundary is not large enough. The hinge loss increases linearly.
그래서 Kuo 다른 제안을 했다. 이는 non linear SSVM을 훈련시키는 접근에서 가장 자연스러운 방법이다. 그에 대한 것을 이제부터 설명해보도록 하겠습니다.
## Efficient Training of Kernel Survival Support Vector Machine
이 방법은 비선형 데이터를 다룰 수 있는 function을 얻는 데에 목표를 가진 것으로 이것의 메인 아이디어는 함수가 새롭게 공식화되어야 하는 것입니다.
즉, 입력값이 실제값에 대응하게 하는 kenrnel function과 관련된 kernel 공간을 생산하여 새로운 function을 찾는 것입니다. 이것도 마찬가지로 hinge loss를 squared hinge loss로 대체했습니다.

Cf)


이 함수식은 또 행렬식으로 표현될 수 있습니다.
이 행렬식으로 보았을 때 아까 본 식에서는 lagrangian multipliers 알파는 제약이 있었지만 베타는 제약이 없는 것을 볼 수 있습니다.

이 비선형 SSVM 함수식은 선형 모델과 유사합니다. 그는 미분한 식을 보면 알 수 있습니다. 이 식은 베타에 대해서 미분이 가능하고 볼록한 형태를 띠고 있습니다. 이렇기 때문에 truncated Newton optimisation이 가능했던 것입니다.

gradient and hessian이 선형 모델과 유사한 속성을 공유하고 있습니다. 그렇기 때문에 선형 모델 SSVM을 훈련시킬 때에도 적용시킬 수 있는 것입니다. 그렇기 때문에 시간이 많이 걸리고 복잡성을 띠고 있는 행렬을 사용하는 것 대신해 이를 사용할 수 있습니다.
##Complexity
linear SSVM의 훈련시키는 알고리즘의 전반적인 complexity

Nbar_cg = average numer of conjugate gradient iterations
N_newton = total numer of Newton updates
비선형 모델을 만들기 위해서는 kernel matrix - K 를 만들어야 합니다. K가 메모리를 저장하지 못하면 매 평가와 실행 때마다 비용과 시간이 듭니다. 그렇기 때문에 몇 가지의 스텝을 밝으면 됩니다.

이는 선형 모델과 다르게 비교할 수 있는 짝들의 합을 구하는 데 더 이상 시간이 많이 드는 작업이 아니게 되었습니다. 만약 샘플들의 수가 적으면 kernel 행렬은 한 번에 계산되고 저장될 수 있습니다. 그러면 cost - O(n^2p)가 됩니다.
따라서 비선형 SSVM 모델을 truncated Newton optimisation and order statistics tress으로 훈련시키는 complexity는 다음과 같이 정리할 수 있습니다.

3. 결론
본문에서는 미리 합성한 데이터와 실제 데이터를 가지고 모델 비교를 했습니다. 저는 간단하게 그 결과 분석표를 가지고 왔습니다.

