[Practical Statistics for Data Scientists] B팀: Hypothesis Testing & Resampling

심화 스터디/Practical Statistics for Data Scientists

[Practical Statistics for Data Scientists] B팀: Hypothesis Testing & Resampling

점핑노루 2022. 3. 31. 23:16

이번 장을 시작하기 전에 chapter3에서 무엇을 배우고 있는지부터 말씀드리고자 합니다.

우리는 전통통계학을 다루고 있습니다. 교재에서는 전통 통계학을 “classical statistics”라고 합니다.

전통통계학은 다음와 같은 파이프라인을 따릅니다.

과거에는 모집단, 즉 전체 데이터에 대한 정보가 없었기에 샘플링 과정을 통해서 모집단의 일부만 추출할 수 있었습니다. 이 샘플링 과정은 우리가 2장 때 배웠던 simple random sampling, stratified random sampling 등 여러 과정이 있겠네요. 이 과정을 통해 얻은 데이터를 바로 샘플이라고 합니다. 샘플은 보통 잘 정제되어있죠.

우리는 샘플을 가지고 각종 통계량도 산출합니다. 기초통계학에서 가장 먼저 배우는 평균, 중위값, 최빈값들이 이 값들에 속하죠. 또한 샘플을 가지고 히스토그램, 박스 플롯 등의 시각화도 합니다.

우리가 샘플을 가지고 이루려는 궁극적인 목표는 모집단을 다시 예측하는 것입니다. Chapter3는 이 부분에 관한 것입니다. 또한 data scientist들은 classical statistical inference를 잘 안쓴다고 하지만, 가끔 쓰는 경우도 있으니 예시들까지 살확인해보실 수 있을 겁니다.

A/B Testing

A/B testing은 2개의 그룹을 비교하는 실험을 의미합니다. 두 그룹의 비교 요인을 우리는 treatment라고 합니다. A/B testing은 위와 같은 과정을 통하여 이루어집니다. 동등한 조건 아래에 있는 특정 sample을 가지고 있다고 생각해봅시다. 예를 들어서 신약의 성능을 기존 약과 비교하는 A/B testing을 했을때, 환자들의 생활습관(흡연, 음주, etc.), 환경 등이 모두 동등하게 놓여져야 하는 거죠.

우리는 이 sample들을 무작위로 다시 2개의 그룹으로 나눕니다. 첫 번째 그룹은 control group으로, 요인을 부여하지 않은 그룹입니다. Control group이 필요한 이유는, 아무런 두 그룹을 임의로 비교했다간 결과가 요인 때문인지 알 수가 없기 때문입니다. 즉 모든 동등한 조건 아래에서 요인만 달라야한다는 거죠. 두 번째 그룹은 treatment group으로, 요인을 부여한 그룹입니다.

신약의 예시를 자세히 들여다볼까요?

신약의 성능을 평가할 때, 최종단계에서는 당연히 사람을 대상으로 임상실험을 진행해야 합니다. 이때 신약이 필요한 사람들을 무작위로 2그룹으로 나눈 다음, 한 그룹에게는 신약을 투여하고 나머지 그룹에는 기존에 투여하던 약, 혹은 위약을 투여하여 그룹을 비교합니다. 그룹 간에 유의미한 차이가 있다면 신약의 효능이 있다는 것이고, 유의미한 차이가 없다면 신약의 효능이 없다는 것을 의미하죠.

또한 A/B test는 두 그룹을 비교하는 것인데, 세 그룹, 네 그룹… 등 그룹이 많아져도 서로 비교가 가능합니다. 그 부분은 ANOVA 파트에서 자세히 살펴볼 수 있습니다.

Hypothesis Testing

Hypothesis testing은 가설검정으로서, 표본을 가지고 모집단의 특정 값이나 분포에 대해서 확률적으로 추론하는 것입니다. 가설 검정을 할 때 우리는 두 가지 가설을 세우게 됩니다.

첫 번째는 귀무가설(Null hypothesis)입니다. 귀무가설은 표본과 모집단의 특성이 일치한다고 제안하는 주장입니다. 예를 들어 대한민국 남성의 평균키는 175cm다가 귀무가설이 되겠죠.

두 번째는 대립가설(Alternative hypothesis)입니다. 대립가설은 귀무가설이 거짓일 때 참이 되는 가설, 혹은 귀무가설과 대립되는 가설입니다. “대한민국 남성의 평균키는 175cm가 아니다”가 대립가설이 되겠죠.그리고 저희는 귀무가설을 바탕으로 검정통계량을 산출하고 p-value를 구함으로써 유의수준 하에 귀무가설이 기각되는지를 살펴보게 됩니다.

다만 대립 가설도 one way hypothesis testing 이나, two way hypothesis testing이냐에 따라 차이가 존재합니다.

One way hypothesis test는 방향이 있는 가설검정이라고 생각하시면 됩니다. 예를들어서 남성의 평균키는 175cm보다 크다, 175cm보다 작다. 가 one way hypothesis test죠.

반면 two way hypothesis test는 방향에 제한을 두지 않은 가설검정입니다. 앞서 대립가설을 설명할 때 들었던 예시 (대한민국 남성의 평균키는 175cm가 아니다)가 대립가설이 되는 것이죠.

그렇다면 one way hypothesis testing이랑 two way hypothesis testing은 언제 사용할까요?

One way hypothesis testing은 방향이 확실할 때 사용합니다. 예를 들어서 대한민국 남성의 평균키가 175cm가 넘는 다는 것을 확신할 때 사용하죠. 하지만 “확실성”을 보장한다는 것은 매우 어렵기 때문에, 대부분 조금 더 보수적인 (더 많은 가능성을 열어두는) two way hypothesis testing을 사용하죠.

Resampling

이번에는 Resampling에 대해서 설명해드리겠습니다. Resampling은 지난주에도 배웠듯 관측된 특정 데이터에서 값을 반복적으로 복원추출하는 것을 의미합니다.

Resampling을 하는 방법은 크게 2가지로 나눌 수 있습니다.

첫 번째 방법은 지난주에 배운 bootstrap 기법입니다. Bootsrap 기법은 반복된 복원추출을 통해 특정 예측값에 대한 의존성을 설명합니다. 예를 들어서 특정 data의 평균을 파악하고 싶을 때, bootsrap 기법을 통해서 sample들의 sample을 반복적으로 추출하면 그것들의 평균이 실제 sample의 평균과 일치하겠죠.

두 번째 방법은 permutation test라는 방법입니다. Permutation test는 2개 이상의 그룹에 대하여 가설검정을 할 때 사용합니다.

Permutation test는 다음과 같은 방법으로 이루어집니다.

간단한 A/B test를 생각해봅시다. 우리는 A/B testing을 통해서 두 그룹 간에 차이가 있는지를 확인하고 싶습니다. 그리고 A그룹에 20개, B그룹에 30개의 데이터가 있다고 가정합시다. 가장 먼저 A그룹이랑 B그룹의 데이터를 합쳐서 50개의 데이터를 만듭니다. 그 다음 50개를 랜덤하게 20/30개로 나누어서 A그룹이랑 B그룹에 배분합니다. 이 때 기존의 샘플 개수랑 일치하게 나누어야 한다는 점 유의하셔야 합니다. 나누어진 데이터를 바탕으로 검정통계량이나 추정값을 산출합니다. 아마 A그룹이랑 B그룹의 차를 구함으로써 파악할 수 있겠죠? 이것이 한 번의 sampling입니다. 저희는 이 permutation test를 여러 번 반복해서 각각의 test statistic/estimate에 대한 분포를 살펴봅니다.

분포가 나왔다면 가장 처음에 가지고 있던 A그룹과 B그룹의 데이터의 차가 분포상 어디에 속하는지를 확인합니다. 만약 그 차가 분포의 끝자락에 위치해 있다면 통계적으로 유의할 확률이 높고, 분포가 집중되어 있는 곳에 위치해 있다면

유의하지 않을 확률이 높겠죠. P-value는 "기존 검정통계량보다 큰 차 / 총 resampling 횟수"로 구할 수 있습니다.

Permutation test에도 여러가지 종류가 있습니다.

첫 번째는 exhaustive permutation test입니다. Exhuastive permutation test는 그룹을 나눌 수 있는 모든 경우의 수를 다 구해서 분포를 만드는 것입니다. 당연히 샘플의 수가 많을 때에는 연산의 과부하 때문에 사용이 어렵습니다. 하지만 더욱 정확한 결과가 나올 수 있다는 장점이 있는 것이죠.

두 번째는 bootstrap permutation test입니다. Bootstrap이랑 permutation test의 아이디어를 합친 방식이라고 생각하면 되는데요, permutation test를 하되 observation들을 모았다가 다시 배분할 때 복원 추출의 방식으로 배분하는

것을 의미합니다.

Permutation test는 모수에 대한 가정이 불확실할 때 사용할 수 있다는 점에서 의의가 있습니다.

R 실습

붓꽃(Iris) 데이터로 꽃잎의 길이(petal length)에 따라 setosa와 versicolor (붓꽃 종류들)이 차이가 있는지 확인하는 permutation test를 진행하였습니다. 코드는 아래와 같습니다.

library(dplyr)
#IRIS 데이터 import
a <- iris

# setosa랑 versicolor을 petal length로 비교 (A/B testing의 일종)
iris_1 <- a %>% 
  select(Petal.Length, Species) %>% 
  filter(Species == 'setosa' | Species == 'versicolor') %>% 
  mutate(index = ifelse(Species=="setosa", 0, 1))

#petal length 변수(value)
petal_length <- iris_1$Petal.Length
#group 변수 (treatment)
index <- iris_1$index


#original difference in means
original <- diff(tapply(petal_length, index, mean))
original

#permutation test 함수 만들기
permutation_test <- function(treatment, value, n){ #n: resampling 횟수
  #빈 리스트 생성
  hist = numeric()
  #그룹 별 비복원 추출로 샘플 뽑은 다음 평균 내서 그 차를 구하는 것. 
  for(i in 1:n){
    hist[i]=diff(tapply(value, sample(treatment, length(treatment), FALSE), mean))
  }
  return(hist)  
}

set.seed(2022)
#5000번의 permutation 
test <- permutation_test(index, petal_length, 5000)
hist(test, breaks=30, main="distribution of permutation test", xlim = c(-1,3))
abline(v=original, lwd=3, col = 'red')

#pvalue 구하기: 검정통계량보다 큰 차 / 전체 개수
sum(original<=(test))/5000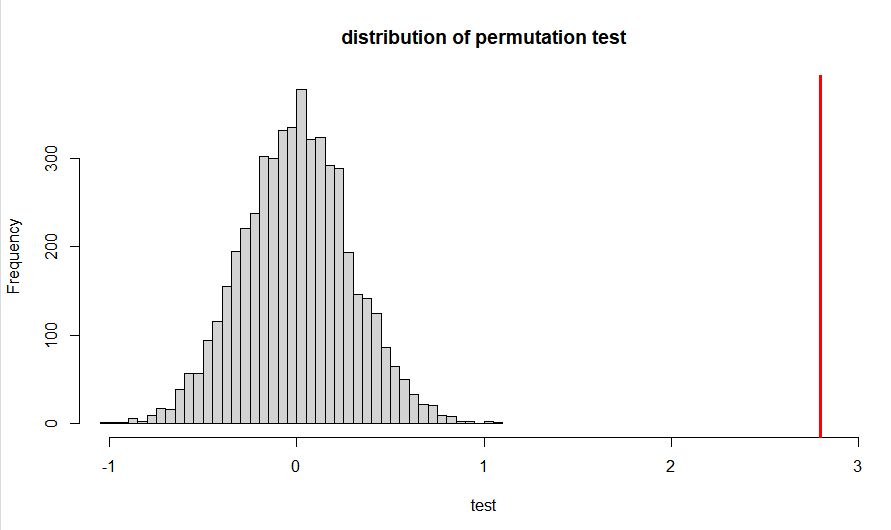

5000번의 permutation test를 했을 때 대부분의 평균의 차가 -1과 1사이에 있었다. 반면 original data의 평균의 차는 2.798로 차이가 컸다.

p-value 산출 결과 0이 나왔고, p-value의 값이 매우 작으므로 꽃잎의 길이에 따라 붓꽃 종류가 다르다고 할 수 있다.