심화 스터디/분류 예측

[분류 예측 스터디]Random Forest paper review

윤뱅 2022. 3. 17. 18:31

작성자 : 채윤병

 

※ Bagging vs Boosting

 

Bagging(Bootstrap aggregating) - 훈련 데이터를 중복 허용하여 랜덤으로 데이터셋을 만드는 과정(Random forest)

Boosting - Error에 기여한 sample마다 다른 가중치를 주어 error를 감소(Adaboost)

 

  Bagging Boosting
목적 분산을 줄이는 것 error를 줄이는 것

아래 위 방향은 bagging의 목적, 오른쪽에서 왼쪽으로의 방향은 boosting의 목적

Introduction

Random forest 이전에도 트리 앙상블을 이용한 예측 향상의 시도가 있었다.

Bagging(1996) -> Random split selection -> Random set of weights(= random selection of a subset of features)

-> Randomness + bagging = Random forest

 

임의 노드 최적화 방식을 통해 학습하는 과정. 각각의 트리 내 존재하는 노드마다 분할 함수를 이용하여 각 노드에서의 정보 획득량이 최대가 되도록 최적화하여 학습하는 방법, k개의 트리들이 각각 발생한 random vector Vk를 이용해 tree를 신장.

 

각각 생성된 Tree-structured classifier(h(x,v_k), k = 1, ...)들의 input x에 대한 분류를 voting -> Random forest의 prediction

2.1 Random forest converge

margin function - 맞게 예측한 것이 다른 클래스로 예측한 것보다 큰 정도를 나타내는 함수

I는 indicatior function -> 1,0을 반환

Margin이 클수록 분류 정확도가 크다.

PE* - Random forest의 generalization error - margin이 0보다 작을 확률

Margin이 0보다 작다 -> 다른 클래스로의 예측이 많다 -> error가 크다.

Law of Large Numbers에 의해 다음 식이 성립한다.

Law of Large Numbers란? - 큰 모집단에서 무작위로 뽑은 표본의 평균이 전체 모집단의 평균과 가까울 가능성이 높다.

 

ex) 동전을 던질 때 앞면이 나오는 경우 1, 아닐 때 0을 나타나는 indicator function I가 있다고 하자. 동전을 N번 던진다고 할 때, N이 무수히 커진다면 I(앞면) -> N/2로 수렴하기 때문에 (1/N)*I(앞면)은 P(앞면)으로 수렴한다.

 

2.2 Strength and correlation

각 분류기의 strength는 앞서 정의했던 margin function의 평균

margin은 맞게 예측한 것이 다른 클래스로 예측한 것보다 큰 정도이기 때문에 클수록 분류를 잘하는 것 -> strength ≒ confidence(확신)

Chebyshev's inequality에 의해 generalization error를 다음과 같이 근사할 수 있음!

Chebyshev's inequality란? - Law of large numbers에서 파생된 개념, 확률 분포를 정확히 모를 때, 평균과 표준 편차로 확률의 값을 근사하는 방식

Chebyshev's inequality에 대한 증명

https://namu.wiki/w/%EC%B2%B4%EB%B9%84%EC%87%BC%ED%94%84%20%EB%B6%80%EB%93%B1%EC%8B%9D

 

var(mr) 또한 근사하는 과정을 거쳐서 generalization error를 correlation과 strength에 대한 근사로 나타낼 수 있다.

-> Random Forest의 일반화 오류를 개별 분류기의 Strength와 Correlation으로 표현할 수 있다!

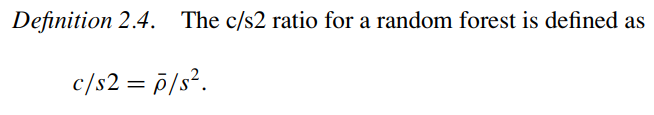
c/s2 - Random forest의 functioning을 나타내는 지표, 작을수록 좋음

 

Theorem에서의 주요한 content

2.1 margin을 정의해서 Law of large numbers를 이용하고 generalization error를 margin에 대한 확률로 나타냈다.

2.2 Chebyshev's inequality를 사용하여 generalization error를 strength와 correlation으로 나타냈다.

3. Using random features

Random forest의 정확도를 높이기 위해서는 strength(margin과 비례)를 높이고 correlation을 낮춰야한다.

 

무작위적으로 선택된 input과 input의 무작위적 combination의 효과

  1.  Adaboost(boosting)만큼 정확도가 좋거나 그보다 더 좋았다.
  2.  이상치나 noise에 대해 영향을 덜 받는다.
  3.  더 빠르다.
  4.  error, strength, correlation, variable importance(변수 중요도)와 같은 유용한 평가
  5.  간단하다.

 

Out of Bag(OOB) estimator - Bagging에서 bootstrap 표본을 만들어 사용할 때, 복원추출을 하기때문에 추출되지 않은 1/3 정도의 데이터를 테스트에 사용하는 방식 => 교차 검증 방식과 유사

 

왜 1/3일까?

n개의 표본을 복원 추출할 때, 특정 표본이 선택되지 않을 확률(1번) : 1-(1/n)

n개의 표본을 복원 추출할 때, 특정 표본이 선택되지 않을 확률(n번) : (1-(1/n))^n

n이 무수히 커지면 (1-(1/n))^n => 1/e ≒ 1/3 에 수렴

즉, 1/3정도가 필연적으로 표본에 사용되지 않음 -> Out of Bag(OOB)

4. Random forests using random input selection(Forest-RI)

Random forest의 randomness -> random input selection(4), linear combinations of inputs(5)

 

CART algorithm이란? - 의사결정트리 알고리즘, 불순도를 측정하여 불순도가 작게 분리하는 방식

불순도 - 지니 불순도

왼쪽 분류의 불순도가 오른쪽 분류의 불순도보다 작으므로 더 바람직한 분류이다.  -> 이러한 분류 방식을 사용하는 알고리즘이 CART 알고리즘

F - Group size(feature)

F를 두가지 값(1, int(logM+1))으로 변화시키며 테스트

Selection - 두 그룹 사이즈에서 가장 낮은 에러율의 평균, Forest-RI single input - 하나의 feature만 트리 신장에 사용, One tree - 하나의 트리만 사용

Random input selection을 하면 adaboost보다 빠르다.

어떠한 경우에서는 single variable을 사용했을 때의 성능이 더 좋았다.

5. Random forests using linear combinations of inputs(Forest-RC)

Input variable에서 무작위적인 선형 결합으로 feature들을 새롭게 정의하는 방식

Selection - 두 그룹 사이즈에서 가장 낮은 에러율의 평균, Two features - F = 2 , One tree - 하나의 트리만 사용

전반적으로 Forest-RI보다 Forest-RC의 성능이 더 좋았다.

☆범주형 변수(categorical variable)가 많을수록 F가 증가하여야 test의 정확도가 증가했다.

6. Empirical results on strength and correlation

실험 목적 - 일반화 오류에 대한 strength와 correlation의 영향 파악

F(input)이 4이상일 때, strength는 유지, input이 커짐에 따라 correlation 증가, error는 feature가 늘어날 때 증가하는 양상을 보임

나머지 결과까지 종합하였을 때, strength가 높고 correlation이 낮아야 error가 작았다.

4, 5번의 randomness의 목적 : strength는 유지하면서 correlation을 낮추는 것

 

Noise 추가하여 학습(8.The effects of output noise)

Adaboost - error 증가, Random forest - Adaboost보다 덜 증가

Why? -> Adaboost는 틀린 instance의 weight를 반복적으로 늘리는 반면 Random forest는 weight에 집중하지 않아 noise에 대한 영향이 더 적다. 

10. Exploring the random forest mechanism

데이터마다 변수의 중요한 정도(feature importance)의 차이가 있다.

왼쪽 - 당뇨병데이터, 오른쪽 - 설문데이터

당뇨병 데이터

- Variable 2만 사용했을 때, error rate : 29.7%

- 모든 variable을 사용했을 때, error rate : 23.1%

- Variable 2 + Variable 8, error rate : 29.4%

- Variable 2 + Variable 6 + Variable 8, error rate : 26.4%

 

설문 데이터

- Variable 4만 사용했을 때, error rate : 4.3% -> 모든 variable을 사용했을 때와 비슷

하나의 특성이 예측에 매우 중요한 역할

 

11~13. Random forest for regression

Regression 또한 classification과 비슷한 방식

Generalization error 정의 -> correlation이 있는 식으로 범위를 정하는 방식

Mean-squared generaliation error for numerical predictor 
Regression에서 generalization error의 정의

Regression이라서 Indicator function이 없다는 것을 제외하고 classification과 동일하다.

Law of Large Numbers에 의해서 Forest의 generalization error가 (12)의 왼쪽과 같은 식으로 표현된다.

Random Forest regression의 성능

Bagging, Adapt bag, Forest의 차이가 정확히 무엇인지는 잘 이해가 안된다..

 

Conclusions

- Random Forest모델의 Randomness가 과적합을 방지했다.

- 분류에서 randomness의 효과가 더 크게 나타났다.

- 큰 데이터에서 random feature에 의한 성능 향상이 작은 데이터보다 더 잘 나타났다.

 

아쉬웠던 점..

Empirical result 시각화 부분

오래된 모델이라서 비교 대조 부분이 예전 기술들이라서 아쉬웠다.