고정 헤더 영역
상세 컨텐츠
본문
작성자: 14기 김혜림, 15기 김지호
참조 논문
Hargreaves, Carol & Chen, Leran. (2020). Stock Prediction Using Deep Learning with Long-Short-Term-Memory Networks.
정종진, 김지연. (2020). LSTM을 이용한 주가예측 모델의 학습방법에 따른 성능분석.
1. 전처리
LSTM을 private 3등한 케이스에서는 데이터 전처리의 비중이 적었는데, 공휴일 데이터 제거, 결측치 처리, feature drop , 데이터 형 변형 정도의 간단한 전처리들이 이루어졌다.
- 행 drop : 토, 일요일과 같은 공휴일은 데이터에서 제거
freq = 'B' : 영업일만 출력하도록 지정.
week_days = pd.DataFrame(pd.date_range(start_date, end_date, freq='B'), columns = ['Date'])
stock_data = pd.merge(week_days, stock_data.drop(columns=['Change']), how = 'left')
- 결측치 처리
주말 외 휴일의 NaN 값을 이전 날의 데이터로 대체하였다.
예측 대상이 되는 10개의 KOSPI 종목 중에서는 학습 기간 내에 상장폐지되는 경우가 없어서 NaN 값을 전날의 종가로 대체하는 방법에 무리가 없다고 판단하였다.
stock_data = stock_data.ffill()사실 종목들의 폐지 날짜 이후의 종가가 NaN이 아닌 마지막 종가로 대체가 되어 학습 데이터에 포함되게 되지만, 성능에 큰 영향은 없었다.
- Feature Selection : 종가만 반영
학습에 사용된 Feature를 고르는 과정에서는 종가만 사용하기로 결정하였다. (나머지 시가, 최고가, 최저가, 거래량 데이터는 drop)
논의 과정에서 거래량의 변화량을 새로운 변수로 도입할지 검토 했으나, 거래량의 변화량을 넣지 않고 종가로만 학습한 모델의 성능(평가지표 : RSME) 이 더 좋았던 선행 연구를 참고하여 거래량 수치도 제외시키기로 결정하였다.

- 데이터 형을 tensor 형(float32) 으로 변환
=> shape = [num_weeks, num_business_days, num_features] 한 데이터 셋 형성
추가적으로 시도해볼만한 다른팀들의 전처리 방법들
- MinMax Scaling
보다 빠르고 안정적인 학습을 위해 scaling 을 진행한 경우가 많았다. 회사마다 주가의 범위가 크게 다르기 때문에 그에 따른 가중치의 스케일도 일관성있게 맞추기 위함이다.
- 주가 지표 추가 - RSI, 볼린저밴드, S&P 500 , kospi, kosdaq
투자자들이 기술적 분석을 시행할 때 주가 지표를 참고하는 경우가 많기 때문에 모델들도 투자자들과 같은 데이터로 학습을 시도한 전처리가 인상적이었다.
- RSI
RSI는 주가의 매수와 매도 압력을 알려주는 지표로, 주가와의 상관계수가 유의미하게 나와서 추가해볼만하다.
def rsi(data, periods = 14, ema = True):
close_delta = data.diff()
up = close_delta.clip(lower=0)
down = -1 * close_delta.clip(lower=0)
if ema == True :
ma_up = up.ewm(com = periods-1, adjust = True, min_periods = periods).mean()
ma_down = down.ewm(com = periods-1, adjust = True, min_periods = periods).mean()
else:
ma_up = up.rolling(windows = periods, adjust = False).mean()
ma_down = down.rolling(windows = periods, adjust = False).mean()
rsi = ma_up / ma_down
rsi = 100 - (100/(1+rsi))
return rsi- 볼린저밴드
볼린저 밴드는 주가가 이동평균선을 따른다는 전제하에 가격의 상대적인 높낮이를 판단할 수 있는 지표다. 이 지표또한 주가와 유의미한 상관관계를 보인다.
def bollinzer_band(data):
k=2
mbb = data.rolling(20).mean() # 중심선 MBB : 이동평균선
MA20_std = data.rolling(20).std()
ubb = mbb + k * MA20_std # 상한선 : 중심선 + 표준편차 * k
lbb = mbb + k * MA20_std # 하한선 : 중심선 - 표준편차 * k
return (ubb,lbb)- s&p 500, kospi, kosdaq
한국의 전체적인 주가는 미국장의 영향을 받기 때문에 s&p 500 지수를 , kospi dhk kosdq의 추세에도 영향을 받기 때문에 이 세 지표를 feature 로 추가함. 데이터를 불러오는 방법은 모두 같다.
# s&p 500
sp = fdr.DataReader('US500', start = start_date , end = end_date)
# kospi
sp = fdr.DataReader('KS11', start = start_date , end = end_date)
# kosdaq
sp = fdr.DataReader('KQ11', start = start_date , end = end_date)
- 데이터셋 구성
시계열 특성을 가진 주가 데이터의 경우 단기간에 급격한 변동을 보이는 경우가 많다. 따라서 시간 순으로 데이터를 나열하고 이를 단순히 7:1:2 (train: val: test) 로 나눈다면 데이터셋의 경향이 달라 올바른 학습이 어려워진다. 이를 해결하기 위해 시간순으로 나열된 데이터를 3: 3: 4의 비율로 나눈 후, 각각의 셋에서 다시 7: 1: 2로 train, val, test set 을 구성하는 방법이 있다. 최종 성능 평가시 이 세 셋의 평균값으로 한다.
이렇게 구성한 데이터셋은 장기적인 주가 예측에서 유리하지만, 이번 대회에서는 1년 이내의 단기간을 학습 기간으로 잡았기 때문에 이러한 데이터셋 분할 방식이 크게 의미 있지는 않은 듯 했다.

2. 모델
- Long Short Term Memory
LSTM은 기존의 RNN 모델의 Vanishing Gradient 문제를 극복하기 위해 개발된 모델로 특히 시계열 문제 및 예측 문제에 뛰어난 성능을 보인다.
구조적으로 은닉층에 입력 게이트, 출력 게이트, 망각 게이트로 이루어진 셀이 추가되었기 때문에 과거의 학습 결과를 기억해뒀다가 새로운 학습에 반영할 수 있게 된다. 따라서 일반적인 선형 모델로는 넣을 수 없는 시간적인 흐름을 LSTM 모델에서는 반영할 수 있게 된다.
( Vanishing Gradient : 딥러닝에서 학습이 길어질 수록 초기 학습한 결과를 잊어버리는 기울기 소실 문제)

- LSTM 사용
class StockPredictor(nn.Module):
def __init__(self, n, h):
super().__init__()
self.seq_encoder = nn.LSTM(
input_size=dim_d*dim_f,
hidden_size=h,
num_layers=n,
bidirectional=False,
batch_first=True
)
self.linear = nn.Sequential(
nn.Flatten(),
nn.ReLU(),
nn.Linear(h, dim_d)
)
def forward(self, x):
x = x.reshape(*x.shape[:2], -1)
x = self.seq_encoder(x)[0]
x = x[:,-1]
return self.linear(x)
- 이때 2개의 stacked lstm(n=2), 8개의 hidden state(h=8)을 이용한 LSTM을 이용함
- LSTM 을 거친 후에는 FC layer를 거쳐서 length = 5(월화수목금) 인 vector를 반환함
3. 학습
def step(batch, training):
x = batch[0].to(device)
y = batch[1].to(device)
if training:
model.train()
output = model(x)
loss = nn.L1Loss()(output, y)
loss.backward()
optimizer.step()
optimizer.zero_grad()
else:
model.eval()
with torch.no_grad():
output = model(x)
loss = nn.L1Loss()(output, y)
return loss.item() * x.shape[0]
def run_epoch(loader, training):
total_loss = 0
for batch in tqdm(loader):
batch_loss = step(batch, training)
total_loss += batch_loss
return total_loss/len(loader.dataset)
train_loss_plot, val_loss_plot = [], []
for epoch in range(num_epochs):
train_epoch_loss = run_epoch(train_loader, training=True)
val_epoch_loss = run_epoch(val_loader, training=False) if num_val>0 else 0
ipd.clear_output(wait=True)
print('epoch' , epoch)
train_loss_plot.append(train_epoch_loss)
val_loss_plot.append(val_epoch_loss)
show_loss_plot(train_loss_plot, val_loss_plot)
if min(val_loss_plot)==val_epoch_loss:
torch.save(model.state_dict(), save_path)
- Adam optimizer를 이용
- L1 loss 를 이용
- 1000epoch, 256 배치 사이즈, 5e-5 lr 이용
4. 결과
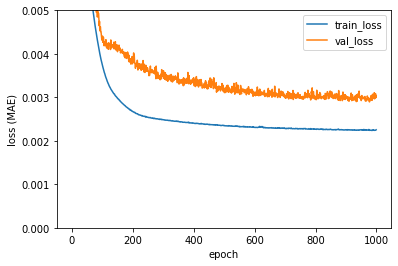
5. 관련 연구
- 1위 모델에 비해서 전처리의 비중이 상당히 적었고, LSTM 을 이용해서 간단하게 모델을 빌드 했음에도 불구하고 높은 성능을 낸 코드. sequence를 갖는 데이터를 분석할 때 이용한 LSTM과 같은 재귀적 딥러닝 방식이 기존의 기법들을 outperform 함을 보여주는 단적인 케이스라고 생각된다.
- 관련해서 찾은 연구: Stock Prediction Using Deep Learning with Long-Short-Term-Memory Networks
본 연구에서는 LSTM을 통해서 주식 가격을 예측했을 때 ARIMA나 regression tree 보다 더 좋은 성능을 냈다는 결론을 내렸다. 뿐만 아니라 market index 에 비해서 높은 수익률을 낼 수 있었다고 한다. 그 이유를 다음과 같이 밝히고 있다: LSTM은 sequential 한 data를 처리하고 유의미한 정보를 뽑아내는데 좋은 모델이다. 나아가서, 더 안정적인 예측값을 도출하는데 이는 ARIMA와 달리 비선형적인 정보도 추출해낼 수 있기 때문이다. 1
- LSTM 외에도 많이 사용된 모델
ARIMA (Auto Regressive Integrated Moving Average) : 자기 상관과 이동편균을 고려한 일변량 시계열 통계 모델인 ARMA 모델을 비안정적인 시계열에도 적용가능하도록 일반화시킨 모델이다. 별도의 validation set 없이 하이퍼 파라미터 튜닝을 진행할 수 있다는 특징이 있다.

- This may be because the LSTM networks is good at processing sequential data, extracting useful information and dropping unnecessary information. Further, the LSTM had a relatively more stable return compared to the ARIMA model. This is because a deep learning model is more capable of extracting the non-linear relationship in the data. In addition, the LSTM model stock portfolio outperformed the stock market index and generated profits over three consecutive time periods [본문으로]
'심화 스터디 > 금융데이터' 카테고리의 다른 글
| [금융데이터 스터디] 데이콘 "주식 종료 가격 예측 경진대회" 코드 리뷰 - 소뉸팀 (0) | 2022.05.29 |
|---|---|
| [금융데이터 스터디] 백테스팅 지표/ 변동성 돌파 전략 (0) | 2022.03.31 |
| [금융데이터 스터디] 트레이딩 전략과 구현 (0) | 2022.03.31 |
| [금융데이터 스터디] 팬더스와 웹 스크레이핑을 사용한 주가 데이터 분석 (0) | 2022.03.17 |





댓글 영역