[분류 예측 스터디] 핸즈온 5장 SVM(Support vector machine)

작성자 : 채윤병

SVM의 핵심 -> 결정 경계

결정 경계를 정하는 방식 1. 라지 마진 분류 2. 소프트 마진 분류

1. 라지 마진 분류 : 도로 경계에 위치한 샘플에 의해 전적으로 결정 경계가 결정되는 방식, 이러한 샘플을 서포트 벡터

 

라지 마진 분류

-> 라지 마진 분류의 단점 : 데이터가 선형적으로 구분될 수 있어야 제대로 작동, 이상치에 민감

이상치가 민감한 라지 마진 분류

SVM은 특성의 스케일에 민감

왼쪽과 오른쪽은 같은 데이터, 단 오른쪽은 정규화를 진행했다. 왼쪽 그림의 결정 경계를 보면 단순히 수평으로 분류하는데 비해 스케일을 조정할 경우 결정 경계가 모든 데이터를 골고루 잘 분류하고 있음을 볼 수 있다.

2. 소프트 마진 분류 : 도로의 폭을(점선의 폭) 넓게 유지하는 것과 마진 오류 사이의 적절한 균형을 위한 분류 방식

 

C float, default=1.0

Regularization parameter. The strength of the regularization is inversely proportional to C. Must be strictly positive. The penalty is a squared l2 penalty.

C가 작아지면 규제(일반화)의 정도가 커짐

비선형 분류

1. 다항 특성

다항특성(Polynomial feature)과 SVC를 파이프라인으로 연결하면 비선형 분류를 할 수 있음!

다항 특성의 딜레마 - 낮은 차수의 다항식은 복잡한 데이터셋을 표현하지 못하고 차수가 높을 경우 특성이 너무 많아짐.. -> 커널 트릭

변환된 벡터의 점곱이 원래 벡터의 접곱의 제곱과 같음 -> 실제 훈련 샘플을 변환할 필요 없이 기존 벡터의 연산을 통해 계산할 수 있음

다항식 커널을 사용한 분류기

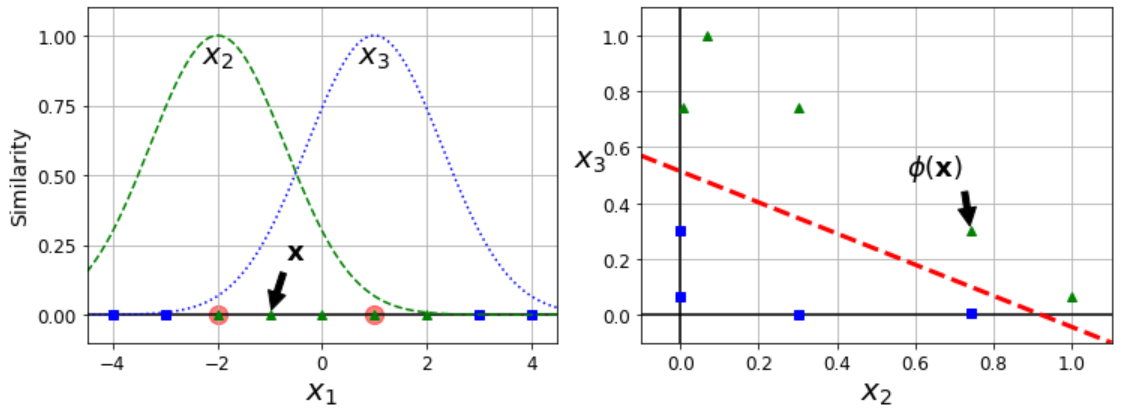
2. 유사도 특성 - 각 샘플이 특정 랜드마크와 얼마나 닮았는가?

L은 랜드마크 지점, gamma는 폭을 결정(작을수록 폭이 넓음)

유사도 계산에는 방사 기저 함수(RBF)가 사용

x1 = -1인 샘플에서 유사도는 x2 = 0.74, x3 = 0.3 그러므로 x2로 분류

 

RBF 커널 코드

gamma는 C와 비슷한 역할 - 그 이유는?

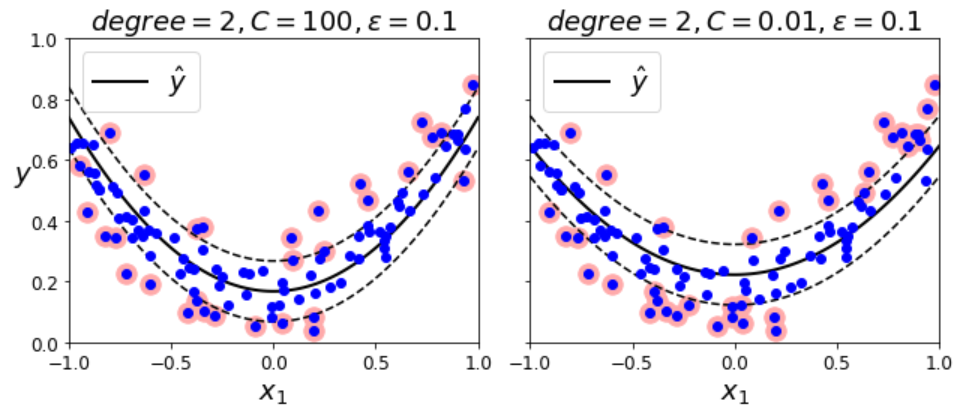
SVM 회귀

SVM 회귀 목적 - 제한된 일정한 마진 오류 안에서 두 클래스 간의 도로 폭이 가능한 한 최대가 되도록 하는 대신, 제한된 마진 오류 안에서 도로 안에 가능한 한 많은 샘플이 들어가도록 학습 -> 도로의 폭은 epsilon으로 조절

epsilon은 도로의 폭을 의미하며 크기에 비례

SVR code

SVM 이론

결정 경계 - 결정 함수와 특성으로 이루어진 평면의 교차점

SVM 분류기의 훈련 = 오류를 하나도 발생하지 않거나(하드 마진) 제한적인 마진 오류를 가지면서(소프트 마진) 가능한 한 마진을 크게하는 가중치 w와 편향 b를 찾는 것

결정 경계의 크기 = ||w||

왼쪽 그림에서 w를 2로 나누면 결정경계는 2배가 됨 -> w와 마진은 반비례

목적 : 마진을 크게 하기 위해서 ||w||를 최소화 하는것, 계산 편의를 의해 1/2*wTw사용

왜 조건이 1보다 커야할까?

소프트 마진은 슬랙 변수를 추가하여 얼마나 마진을 위반할지 정함

마진 오류를 최소화하기 위해 가은한 한 슬랙 변수의 값을 작게 만드는 것 vs 마진을 크게 하기 위해 1/2wTw를 가능한 한 작게 만드는 것

->C가 그 정도를 결정

% 원문제와 쌍대문제 - 원 문제라는 제약이 있는 최적화 문제가 주어지면 쌍대 문제라고 하는 깊게 관련된 다른 문제로 표현할 수 있다. 쌍대 문제의 해는 원 문제 해의 하한값이지만 어떤 조건하에서는 원 문제와 똑같은 해를 제공한다. SVM은 이 조건을 만족하기 때문에 원 문제의 해를 쌍대 문제로 풀 수 있다. 쌍대 문제는 원 문제에서는 적용이 안 되는 커널 트릭을 가능하게 한다.