[분류 예측 스터디] XGBoost : A Scalable Tree Boosting System

작성자: 김제성

논문 : http://dmlc.cs.washington.edu/data/pdf/XGBoostArxiv.pdf

1. Introduction

• XGBoost의 가장 큰 장점 중 하나는 다양한 시나리오에 접목시킬 수 있는 확장성(Scability)이 존재하다는 것이다. 

• 이러한 확장성을 달성하기 위해 새로운 tree boosting(ch.2) 알고리즘(ch.3)과 해당 알고리즘을 결정하는 최적화 시키는 시스템(ch.4)이 제시되었다. 

---

2. Tree Boosting In A Nutshell

2.1 Regularized Learning Objective

• XGBoost 모델에서 base learner는 CART(Classification and Regression Tree)가 사용된다. 
• 여기서 예측값 ŷ은 Φ(xi)로 나타낼 수 있는데 개별 트리에서 결정된 x의 가중치들의 합 형태(additive function)로 표현된다. (tree boosting이기 때문에 가중치 결과물로 나온다는 점을 유의해야 한다)

w는 최종 잎에서 x의 가중치를, q는 트리의 구조 혹은 quality를 나타낸다.

• 여기까지가 일반적인 tree boosting 개념이었다면 XGBoost에선 여기에 규제항(Regularization)을 더해준다. 규제항을 더해주는 이유는 다음과 같다.

▷ CART Tree 담고 있는 공간 F에서 새로운 함수 f_k(x_i)를 뽑는 근거가 된다. (이는 Loss Function을 최소화시키는 f(x)로 선정이 된다)

▷ 규제항은 모델의 복잡도를 방지하기 위해 새로 뽑힌 f(x)의 복잡도가 높다면 규제항 값이 증가함으로써 그 함수를 선택하지 않게 유도한다. (패널티 부여)

▷ 모델의 복잡도를 방지한다는 것은 모델이 데이터에 오버피팅 되는 것을 방지하고 그에 따른 variance를 줄이고자 하는 것을 의미한다.

 

• 그렇다면 우리가 모델을 만들기 위해 여기서 알아내야 하는 것은 w(각 leaf에서의 가중치)와 q(tree의 structure 혹은 quality)이다. -> 목적 함수를 뜯어보면서 두 파라미터를 알아내자

q를 어떤 변수가 아닌 하나의 tree라고 이해하면 된다. 어느 지점에서 어느 분할점을 갖고 있는 특정 트리 q

 

2.2 Gradient Tree Boosting

• 규제화된 목적함수 L(Φ)는 또다른 함수Φ를 파라미터로 받고 있기 때문에 유클리디안 공간을 통해 최적화 할 수 없다. → Gradient를 이용해 함수를 간단한 형태로 바꾸어 최적화시킨다.

▷(해석) Loss function의 최솟값을 구하고 싶은데 그 자체가 너무 복잡하기 때문에 테일러급수를 활용해 이를 간단한 다항함수 형태로 바꾸어주고 경사하강법을 통해 최적의 지점을 찾아낸다.

g는 loss function의 도함수이고, h는 loss function의 이계도함수이다.

• 위 식을 풀어내는 과정에서 각 leaf의 최적 weight값을 구할 수 있고, 그 weight값을 다시 목적함수에 넣어 얻은 optimal value는 tree의 구조(q) 의 성능을 나타내는 수식을 나타낸다.

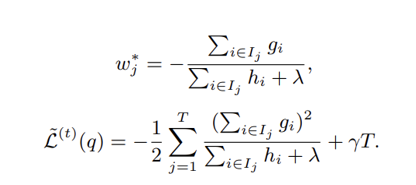
▷위 식을 통해 얻어 낼 수 있는 것은 Loss Reduction 혹은 Gain으로 분지점에서 다시 가지를 내리는 split과정을 판단하는 척도를 만들어낼 수 있다.

• L_split < 0 : split을 하지 않았을 때 더 많은 loss reduction을 얻을 수 있다(=split 중지) (무한히 split을 하게 되면 overfit 되니까)
• 분지 과정에서 여러개의 L_split 값들이 나올텐데 그 중에서 감소폭(=loss reduction=gain)이 가장 큰 분할을 고르면 되고 분지(split)를 하는 방법을 3장에서 다룬다.

2.3 Shrinkage and Column SubSampling

• Shrinkage : 새롭게 추가되는 tree에 weight를 추가로 더한다.     

          ▷개별 트리의 영향력을 줄이고 미래 트리를 위한 공간을 남긴다.     

• Column Subsampling : RF처럼 feature를 일부 추출해서 사용한다.

          ▷데이터에 다양성을 부여하여 계산 속도를 높이고 과대적합을 방지한다.

 

---

 

3. Split Finding Algorithms

3.1 Basic Exact Greedy Algorithm

• 모든 feature들에 대해 일일이 가장 좋은 분할변수 분할점 찾는 split을 진행한다. (위에서 구한 L_split이 가장 크게 나오는 split을 찾는다)
• 그나마 효율적으로 하기 위해 feature을 값의 크기에 따라 미리 정렬(sorting)을 해준다

          ▷최적해는 보장 되지만 메모리 용량, 계산량 측면에서 효율이 매우 안 좋다.

 

3.2 Approximate Algorithm

• value를 sort한 뒤, 데이터를 몇 개의 묶음(bucket)으로 나누어 병렬적으로 계산하면서 최적의 분할점을 찾는다.

( 데이터 묶음을 논문에서는 Percentile이라는 용어를 통해 설명하고 있다)

         

          ▷근사적으로 최적해를 찾게 되지만 병렬적인 계산이 가능해지면서 계산 속도의 향상을 얻을 수 있다.

• Split 지점 찾은 뒤 다음 묶음은 어떻게 처리할 것인지 따라서 Global variant(split 이후에도 처음 묶음 그대로 유지)와 Local variant(첫번째 split통해 나눠진 다음에 개별적으로 또 이전에 정의된 개수대로 묶음 진행)로 나뉜다.

global variant에서는 더 많은 묶음들을 만들어내는 것이 유용하고, local variant에서는 bigger tree에서 적용하는 것이 유용하다.

 

 

 

3.3 Weighted Quantile Sketch

 

3.4 Sparsity-aware Split Finding

• 대부분의 실제 데이터들은 dense(모든 관측치, 열에 빠진 부분이 없는)하지 못하고 sparse(결측치 존재, 0값이 많을때, 원핫인코딩할 때)한 경우가 많기 때문에 이러한 패턴들을 모델이 인지할 수 있도록 하는 알고리즘이다. 
• How? 각 트리노드 마다 sparse data만 각각 왼쪽 노드, 오른쪽 노드로 보내보고 score를 구해서 더 높은 값을 보인 방향으로 default direction을 지정한다. 

          ▷이렇게 sparse data를 인지한 형태로 처리함으로써 아주 빠른 속도로 데이터를 처리할 수 있게 된다. 

---

 

4. System Design

4.1 Column Block for Parallel Learning

• 트리 학습 과정에 있어 많은 시간 비용이 소모되는 데이터 정렬을 위해, block이라는 메모리 단위로 정렬을 진행하는 Compressed Column (CSC) 방식이 제안된다.  (특이하게 결측치 값들은 sorting 과정에서 배제되면서 최종 store되는 데이터 개수가 줄어든다)

 

• Greedy Algorithm에서
  • 모든 column 데이터가 하나의 block안으로 들어가 정렬이 된 상태에서 split finding을 진행한다.
  • (결론적으로 데이터의 value가 index처럼 활용되어 정렬이 되지만 개별 데이터 value가 지니고 있는 통계량들은 그 자리에 계속 머물기 때문에 포인터처럼 처리되면서 메모리를 아낀다는 의미로 해석된다.)

 

• Approximate Algorithm에서
  • (행 단위로 끊어서) 여러 개의 block들을 만들어 병렬적으로 각 block들에 대해 split 지점을 알아낸 뒤 그것들을 한 번에 선형적으로 탐색(linear scan)하여 최종 split 지점을 선정하게 된다.

 

 

• Block Structure를 사용하게 되면 시간 복잡도 (Time Complexity) 측면에서도 매우 효율적인 것으로 보인다.

 

 

4.2 Cache-aware Access

• 데이터가 가지고 있는 통계값(L_split구하기 위해 필요했던 G,H)을 여타 디스크 같은 곳이 아니라 CPU cache에 보관하여 연속적인 메모리 형태(이를 통해 데이터 간 longer dependency가 형성됨)로 만들고 이는 알고리즘 처리 속도를 높인다.

 

4.3 Blocks for Out-of-Core Computation

• 모든 데이터를 간편하게 cache에서만 사용할 수 없고 메인 메모리에 들어맞지 않는 데이터가 존재하기도 한다.
• 그러한 데이터는 디스크를 땡겨다가 써야하는데(out-of-computation) 이를 효율적으로처리 하기 위해서 block compression, block sharding 이라는 전처리 기법을 사용한다. 

---

5. Related Works

• 개별 트리 모델 -> Gradient Boosting , Regularized model, Column Sampling 
• 알고리즘 -> Sparsity-aware Learning 
• 시스템 -> Parallel Tree Learning

 

---

6. End to End Evalutaions

▷분류 문제에서 월등히 높은 처리 속도를 보여주었다.

 

▷XGBoost는 greedy algorithm으로 pGBRT는 approximate algorithm으로 해결했음에도 XGBoost가 더 빠른 속도를 보였다. 이는 알고리즘을 구축하는 시스템 환경 설정 과정에서 진행된 column subsampling의 영향 덕분인 것으로 보인다.

 

---

7. 결론 및 느낀점

 

1)개별 트리모델을 구축하는 방법

2) 트리 split을 위해 필요한 알고리즘

3) 알고리즘의 효율을 위한 시스템 배치

이렇게 세 흐름으로 논문에서 XGBoost를 설명하고 있었다. 이러한 흐름으로 구축이 된 XGBoost는 매우 빠른 처리 속도와 다양한 형태의 데이터에 대한 적응을 보장할 수 있다. 

 

논문리뷰 과정에서 생각보다 캐시와 같이 컴퓨터 메모리나 하드웨어적인 부분에서 많은 언급이 있어서 해석에 어려움이 있었다. 그리고 GBM 설명 과정에서 '잘못된 데이터에 가중치를 부여하고 residual을 사용해 tree 모델을 만들어간다'라는 해석을 기대하고 읽었는데 정작 그런 부분은 생략이 되고 오로지 수학적 수식을 위해 gradient가 언급만 된 느낌이라 이해를 하는데 많은 시간이 필요했던 것 같다. 

 

 

 

Reference

- https://exupery-1.tistory.com/183

[Ensemble] XGBoost, 극한의 가성비

- https://github.com/pilsung-kang/Business-Analytics-IME654-/blob/master/04%20Ensemble%20Learning/04-7_Ensemble%20Learning_XGBoost.pdf

GitHub - pilsung-kang/Business-Analytics-IME654-: Course homepage for "Business Analytics (IME654)" @Korea University

- https://www.youtube.com/watch?v=VkaZXGknN3g&list=PLetSlH8YjIfUpPbSAfsY4zBJfztlH9CSQ&index=58 

같이 보면 좋을 코딩 자료

- https://www.kaggle.com/code/lifesailor/xgboost/notebook

Xgboost 하이퍼 파라미터 튜닝

https://www.analyticsvidhya.com/blog/2016/03/complete-guide-parameter-tuning-xgboost-with-codes-python/

XGBoost Parameters | XGBoost Parameter Tuning